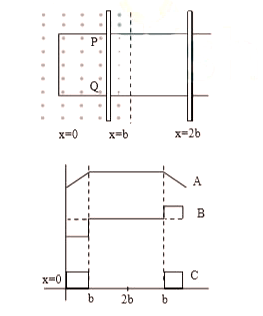
In the following diagram, the arm PQ of the rectangular conductor is moved from x = 0 ,
outwards.
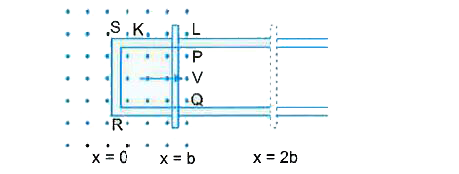
The unfirom magnetic field is perpendicular to the plane and extends from x=0 to x=b and is zero for x>b. Only the arm PQ possesses substantial resistance 'r'. Consider the situation when the arm PQ is pulled outwards from x = 0 to x = 2b, and then moved back to x = 0 with constant speed 'v'. Obtain expressions from the (i) magnetic flux, (ii) the induced emf, (iii) the force necessary to pull the arm and (iv) the power dissipated as joule heat.
Sketch the variation of these quantities with distance.
As per figure given with the question let us first consider the forward motion from x= 0 to x = 2b.
(i) Magnetic flux ϕB linked with the circuit SPQR will be ϕB=Blx for 0≤x≤b and ϕB=Blb for b≤x≤2b.
(ii) The induced emf ε=dϕBdt is
ε=−Blv for 0≤x≤b
andε=0 for b≤x≤2b.
(iii) When ε is non - zero induced current I=εr.
∴ Force required to keep the arm PQ in constant notion will be F=IlB towards left.
Thus, F=B2l2vr for 0≤x≤bandF=0 for b≤x≤2b
(iv) Power dissipalated as Joule heat P=I2r
So, P=B2l2v2r for 0≤x≤b
and P=0 for b≤x≤2b.
For inward motion from x = 2b to x = 0, we get similar results.
The variation of ϕB,E,FandP with x si shown in the figure.

Topper's Solved these Questions
- CBSE SAMPLE QUESTION PAPER 2019-20 (SOLVED)BOOK - U-LIKE SERIESCHAPTER - CBSE SAMPLE QUESTION PAPER 2019-20 (SOLVED)EXERCISE - SECTION C
8 Videos
- CBSE EXAMINATION PAPER 2020 (SOLVED) BOOK - U-LIKE SERIESCHAPTER - CBSE EXAMINATION PAPER 2020 (SOLVED) EXERCISE - SECTION - D
6 Videos
- CURRENT ELECTRICITY BOOK - U-LIKE SERIESCHAPTER - CURRENT ELECTRICITY EXERCISE - SELF ASSESSMENT TEST (SECTION C )
3 Videos
Similar Questions
The arm PQ of the rectangular conductor is moved from x=0, outwards in the uniform magnetic field which extends from x=0 to x=b and is zero for x>b as shown. Only the arm PQ possess substantial resistance r. Consider the situation when the arm PQ is pulled outwards from x=0 to x=2b, and is then moved back to x=0 with constant speed v. Obtain expression for the flux, the induced emf, the force necessary to pull the arm and the power dissipated as Joule heat. Sketch the variation of these quantities with distance.
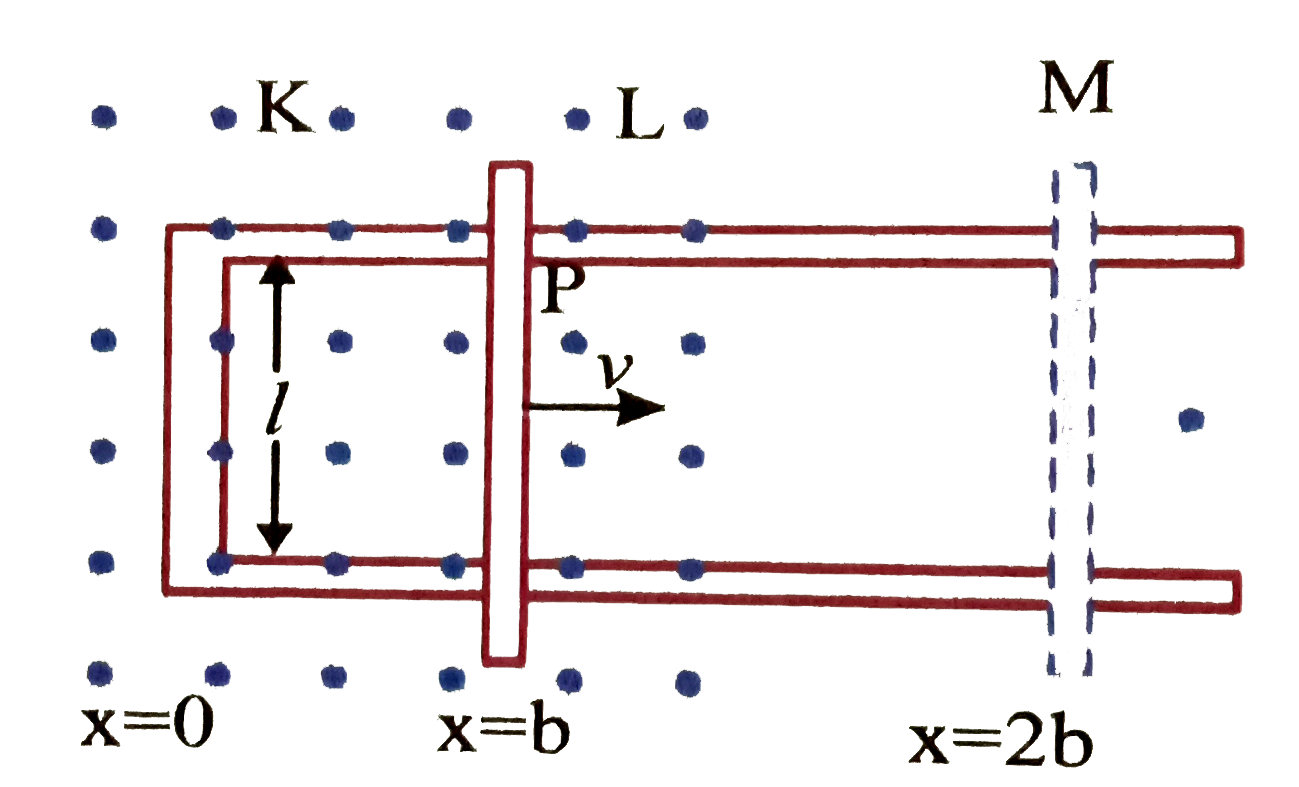
View SolutionThe arm PQ of the rectangular conductor is moved from x=0, outwards in the uniform magnetic field which extends from x=0 to x=b and is zero for x>b as shown. Only the arm PQ possess substantial ressitance r. Consider the situation when the arm PQ is pulled outwards from x=0 to x=2b, and is then moved back to x=0 with constant speed v. Obtain expression for the flux, the induced emf, the force necessary to pull the arm and the power dissipated as Joule heat. Sketch the variation of these quantities with distance.

View Solution
Knowledge Check
The area between the arms of the curve |y|=x3 from x=0 to x=2 is
A2B4C8D16
(a) State Faraday's law of electromagnetic induction.
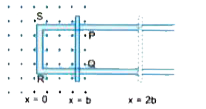
(b) Figure 6.60 shows a rectangular conductor PQRS in which the conductor PQ is free to move in a uniform magnetic field B perpendicular to the plane of the paper. The field extends from x = 0 to x =b and is zero for >b. Assume that only the arm PQ possesses resistance r. When the arm PQ is pulled outward from x =0 to x = 2b and is then moved backward to x = 0 with constant speed v, obtain the expressions for the flux and the induced emf. Sketch the variations of these quantities with distance 0≤x≤2b.
View SolutionIn the situation shown, the current in arm PQ will be
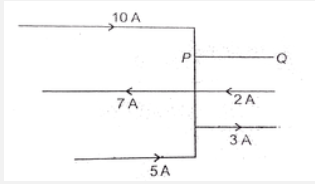
View SolutionIn the situation shown, the current in arm PQ will be

View SolutionState Faraday's law of electromagnetic induction.
Figure shows a rectangular conductor PQRS in which the conductor PQ is free to move in a uniform magnetic field B perpendicular to the plane of the paper.The field extends from x=0 to x=b and is zero for x>b.Assume that only the arm PQ posses resistance r.When the arm PQ is pulled outward from x=0 with constant speed v, obtain the expressions for the flux and the induced emf. sketch the variations of these quantities with distance 0≤x≤2b.

View SolutionState Faraday's law of electromagnetic induction.
Figure shows a rectangular conductor PQRS in which the conductor PQ is free to move in a uniform magnetic field B perpendicular to the plane of the paper.The field extends from x=0 to x=b and is zero for x>b.Assume that only the arm PQ posses resistance r.When the arm PQ is pulled outward from x=0 with constant speed v, obtain the expressions for the flux and the induced emf. sketch the variations of these quantities with distance 0≤x≤2b.

View SolutionThe area between the arms of the curve |y|=x3 from x=0 to x=2 is
View SolutionThe arm PQ of a rectangular conductor is moving from x = 0 to x = 2b outwards and then inwards from x = 2b to x = 0 as shown in the figure. A uniform magnetic field perpendicular to the plane is acting from x = 0 to x = b. Identify the graph showing the variation of different quantities with distance :
View Solution
