Using Gauss' law deduce the expression for the electric field due to a uniformly charged sperical conducting shell of radius R at a point (i) outside and (ii) inside the shell.
Plot a graph showing variation of electric field as a function of r>Randr<R. (r being the distance from the centre of the shell)
Electric field due to a uniformly charged thin spherical shell -
(i) When point P lies Outside the Spherical Shell - Suppose that we have to calculate electric field at the point P at a distance r(r>R) from its centre. Draw the Gaussian surface through point P so as to enclose the charged spherical shell of radius r and centre O.
Let →E be the electric field at point P. Then, the electric flux through area element →ds is given by,
dϕ=→E.→ds
Since →ds is also along normal to the surface,
dϕ=Eds
∴ Total electric flux through the Gaussian surface is given by,
ϕ=∮Eds=E∮sds
Now,
∮ds=4πr2
∴ ϕ=E×4πr2 ...(i)
Since the charge enclosed by the Gaussian surface is q, according to Gauss theorem,
ϕ=qε0 ...(ii)
From equations (i) and (ii), we get
E×4πr2=qε0
E=14πε0.qr2 (for r>R)

(ii) When point P lies inside the spherical shell : In such a case the Gaussian surface encloses no charge
According to Gauss Law,
E×4πr2=0
i.e., E=0(r<R)
Graph showing the variation of electric field as a function of r.
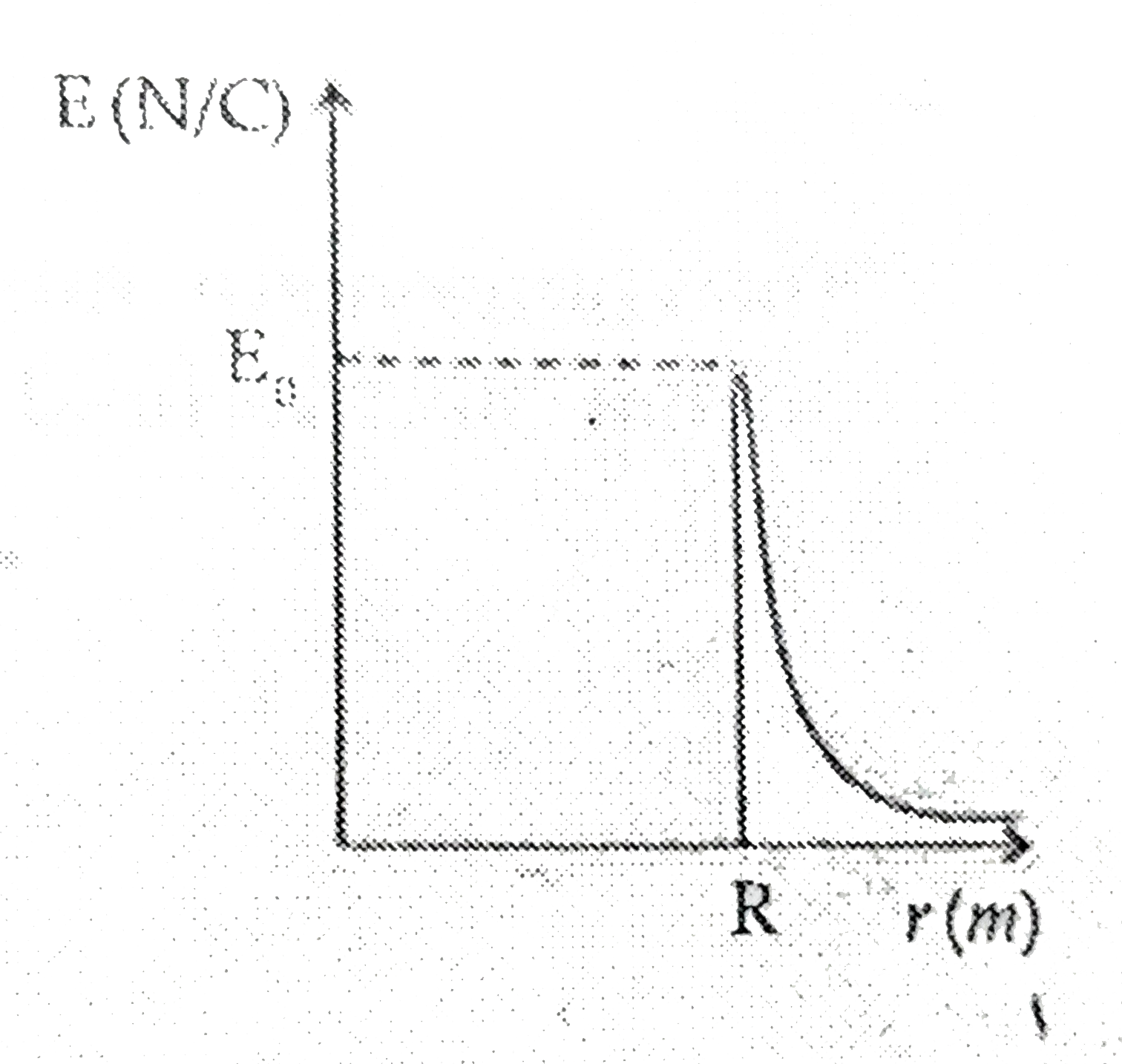
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SET-II
35 Videos
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SET-III
25 Videos
- XII BOARDSBOOK - XII BOARDS PREVIOUS YEARCHAPTER - XII BOARDSEXERCISE - SET III
9 Videos
- SAMPLE PAPER 2019BOOK - XII BOARDS PREVIOUS YEARCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
Using Gauss' law deduce the expression for the electric field due to uniformaly charged spherical conducting shell of radius R at point (i) outside ,and (ii) inside the shell.
Plot a graph showing variation of electric field as a functions or r for r< R and .(r being the distance from the centre of the shell).
View SolutionUsing Gauss's law obtain the expression for the electric field due to uniformly charged thin spherical shell of radius R at a point outside the shell. Draw a graph showing the variation of electric tield with r, for r gt R and r lt R.
View Solution
Knowledge Check
Which of the following graph represents the variation of electric field E due to a thin charged spherical shell of radius R as a function of the distance r from the centre of the shell?
A B
B CD
CD
Using Gauss's law obtain the expression for the electric field due to uniformly charged thin spherical shell of radius R at a point outside the shell. Draw a graph showing the variation of electric tield with r, for r gt R and r lt R.
View SolutionUsing Gauss's law obtain the expression for the electric field due to uniformly charged thin spherical shell of radius R at a point outside the shell. Draw a graph showing the variation of electric tield with r, for r gt R and r lt R.
View SolutionFind the gravitational potential due to a spherical shell of mass M and radius R at r<R and r>R, where r is the distance from the centre of the shell.
View SolutionFind the gravitational potential due to a spherical shell of mass M and radius R at r<R and r>R, where r is the distance from the centre of the shell.
View SolutionUsing Gauss’s theorem in electrostatics, deduce an expression for electric field intensity due to a charged spherical shell at a point (i) inside (ii) on its surface (iii) outside it. Graphically show the variation of electric field intensity with distance from the centre of shell.
View SolutionDraw a graph of electric field E(r) with distance r from the centre of the shell for 0≤r≤0 .
View SolutionA metallic spherical shell of radius R has a charge -Q on it. A point charge +Q is placed at the centre of the shell. Which of the graphs shown below may correctly represent the variation of electric field E with distance r from the centre of shell ?
View Solution
