A metallic spherical shell of radius R has a charge -Q on it. A point charge +Q is placed at the centre of the shell. Which of the graphs shown below may correctly represent the variation of electric field E with distance r from the centre of shell ?


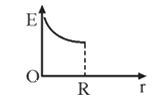
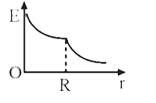
The correct Answer is:C
To solve the problem, we need to analyze the electric field E at different distances r from the center of a metallic spherical shell with a charge −Q and a point charge +Q placed at its center.
1. Understanding the Setup:
- We have a metallic spherical shell of radius R with a charge of −Q.
- A point charge +Q is placed at the center of the shell.
- We need to find the variation of the electric field E with distance r from the center.
Hint: Visualize the setup with a diagram showing the shell and the point charge.
2. Electric Field Inside the Shell (r < R):
- According to Gauss's law, the electric field inside a conductor in electrostatic equilibrium is zero.
- For r<R, the only charge enclosed by a Gaussian surface is the point charge +Q.
- The electric field E at a distance r from the center can be calculated using the formula:
E=kQr2
- Here, k is Coulomb's constant.
Hint: Remember that the electric field inside a conductor is zero, but inside the cavity (where the point charge is), it is determined by the point charge.
3. Electric Field on the Surface of the Shell (r = R):
- At the surface of the shell, the electric field is given by:
E=kQR2
- This is the electric field just at the surface.
Hint: The electric field is not zero at the surface; it is determined by the charge enclosed.
4. Electric Field Outside the Shell (r > R):
- For r>R, the total charge enclosed by a Gaussian surface is +Q+(−Q)=0.
- Therefore, the electric field E outside the shell is zero:
E=0
Hint: For distances greater than the radius of the shell, consider the net charge enclosed.
5. Graphing the Electric Field:
- For r<R, the electric field E is inversely proportional to r2 and approaches infinity as r approaches zero.
- At r=R, the electric field is at a finite value kQR2.
- For r>R, the electric field drops to zero.
Hint: Sketch the graph based on the behavior of E in the three regions: inside, on the surface, and outside the shell.
Conclusion:
The graph representing the variation of electric field E with distance r from the center of the shell should show:
- An increasing electric field as r approaches zero,
- A finite value at r=R,
- A drop to zero for r>R.
The correct graph would depict these characteristics, confirming that the electric field is zero outside the shell and behaves according to the inverse square law inside the cavity.
- We have a metallic spherical shell of radius R with a charge of −Q.
- A point charge +Q is placed at the center of the shell.
- We need to find the variation of the electric field E with distance r from the center.
- According to Gauss's law, the electric field inside a conductor in electrostatic equilibrium is zero.
- For r<R, the only charge enclosed by a Gaussian surface is the point charge +Q.
- The electric field E at a distance r from the center can be calculated using the formula:
E=kQr2
- Here, k is Coulomb's constant.
- At the surface of the shell, the electric field is given by:
E=kQR2
- This is the electric field just at the surface.
- For r>R, the total charge enclosed by a Gaussian surface is +Q+(−Q)=0.
- Therefore, the electric field E outside the shell is zero:
E=0
- For r<R, the electric field E is inversely proportional to r2 and approaches infinity as r approaches zero.
- At r=R, the electric field is at a finite value kQR2.
- For r>R, the electric field drops to zero.
The graph representing the variation of electric field E with distance r from the center of the shell should show:
- An increasing electric field as r approaches zero,
- A finite value at r=R,
- A drop to zero for r>R.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE MAIN
65 Videos
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced (Archive)
89 Videos
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - LEVEL - 1
105 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - IMPECCABLE
52 Videos
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE
1 Videos
Similar Questions
Which one of the following graphs represents the variation of electric field with distance r from the centre of a charged spherical conductor of radius R?
View SolutionIf r is distance measured from centre of a charged shell and R is its radius, then the graph which may correctly represent variation of electric field (E) is
View Solution
Knowledge Check
A spherical insulator of radius R is charged uniformly with a charge Q throughout its volume and contains a point charge Q16 located at its centre. Which of the following graphs best represents qualitatively, the variation of electric field intensity E with distance r from the centre?
A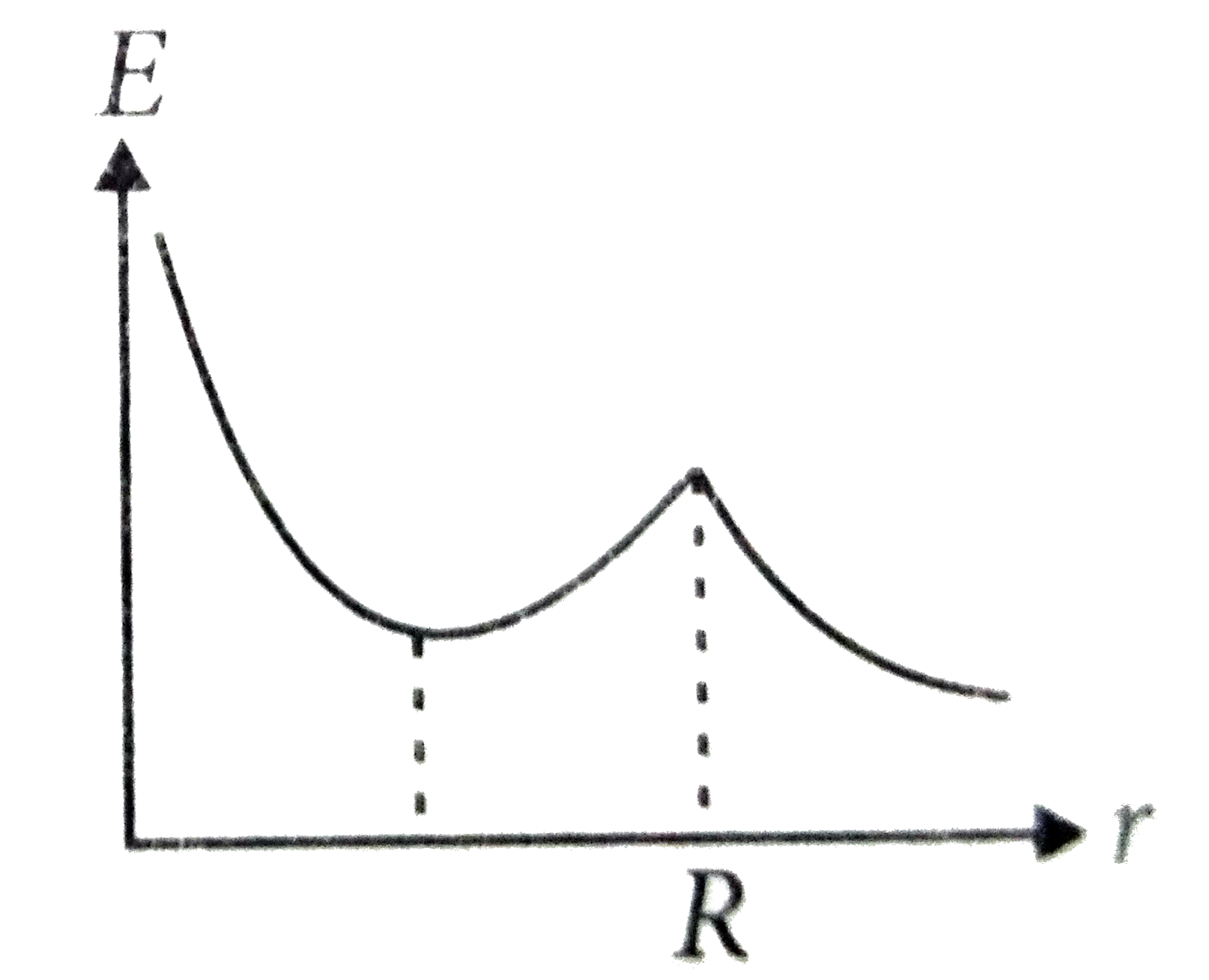 B
B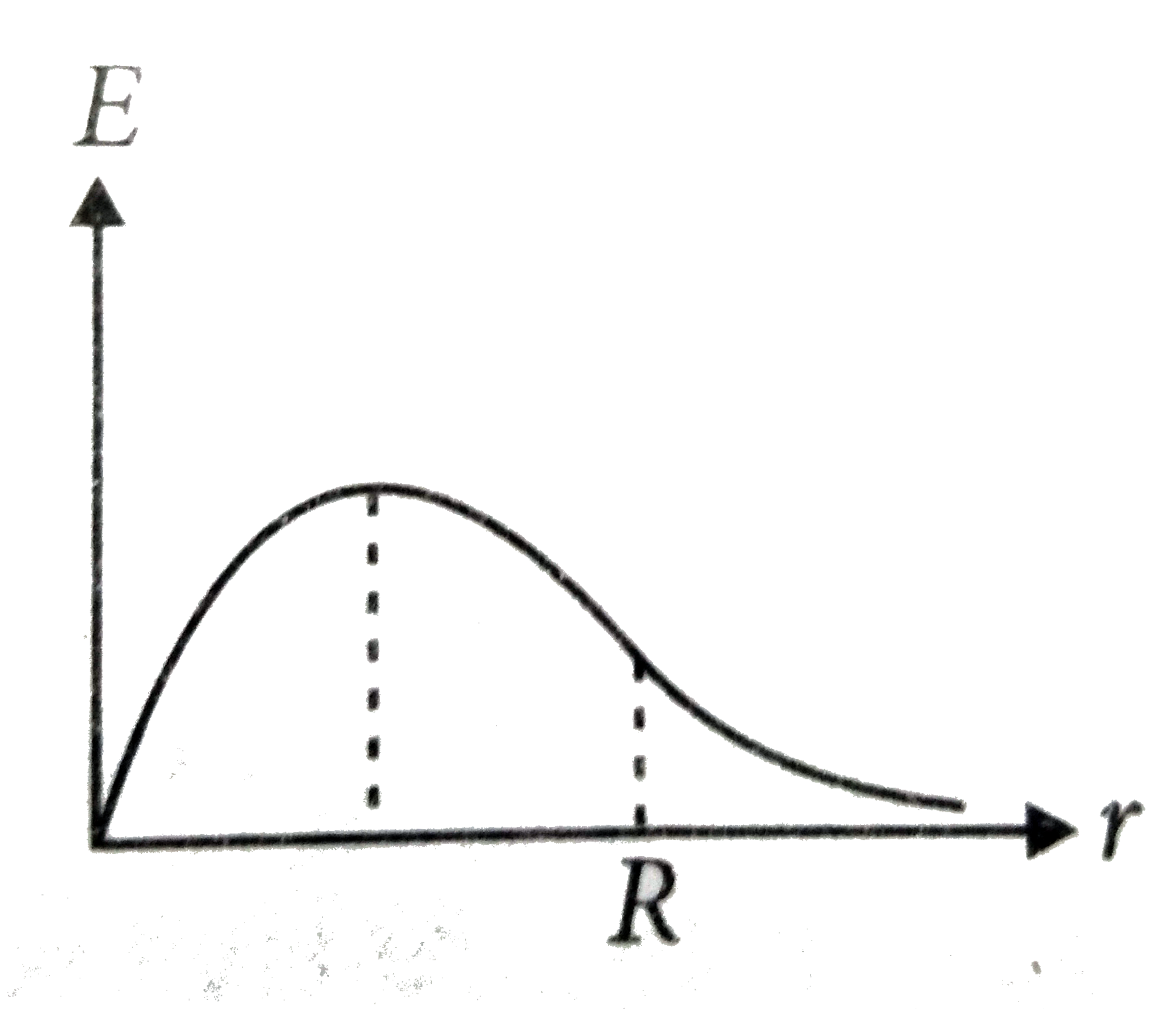 C
C D
D
A thin spherical conducting shell of radius R has a charge q. Another charge Q is placed at the centre of the shell. The electrostatic potential at a point P a distance R2 from the centre of the shell is
View SolutionA thin spherical conducting shell of radius R has a charge q. Another charge Q is placed at the centre of the shell. The electrostatic potential at a point P a distance R/2 from the centre of the shell is
View SolutionA point charge is kept at the centre of a metallic insulated spherical shell. Then
View SolutionA point charge is kept at the centre of a metallic insulated spherical shell. Then
View SolutionA charge Q is uniformly distributed in a dielectric sphere of radius R (having dielectric constant unity). This dielectric sphere is enclosed by a concentric spherical shell of radius 2R and having uniformly distributed charge 2Q. Which of the following graph correctly represents variation of electric field with distance r from the common centre?

View SolutionA thin metallic spherical shell contains a charge Q on it. A point charge q is placed at the center of the shell and another charge q1 is placed outside it as shown in the figure. All the three charges are positive. Find the force on the charge

a. at centre due to all charges.
b. at center due to shell.
View SolutionA conducting shell of radius R carries charge–Q. A point charge +Q is placed at the centre of shell. The electric field E varies with distance r (from the centre of the shell) as :
View Solution
