If the current through a resistor in a circuit increases by 3%, the power dissipated by the resistor
increases approximately by 3%
increases approximately by 6%
increases approximately by 9%
decreases approximately by 3%
The correct Answer is:B
To solve the problem of how the power dissipated by a resistor changes when the current through it increases by 3%, we can follow these steps:
1. Understanding the Power Formula:
The power (P) dissipated by a resistor is given by the formula:
P=I2R
where I is the current through the resistor and R is the resistance.
2. Identifying the Change in Current:
We are given that the current increases by 3%. This can be expressed as:
ΔI=0.03I
where ΔI is the change in current.
3. Calculating the New Current:
The new current I′ after the increase can be written as:
I′=I+ΔI=I+0.03I=1.03I
4. Calculating the New Power:
The new power P′ after the increase in current can be calculated using the new current:
P′=(I′)2R=(1.03I)2R=1.0609I2R
5. Finding the Percentage Change in Power:
The original power P is:
P=I2R
The change in power ΔP is:
ΔP=P′−P=(1.0609I2R)−(I2R)=0.0609I2R
The percentage change in power can be calculated as:
Percentage Change in Power=(ΔPP)×100=(0.0609I2RI2R)×100=6.09%
6. Conclusion:
Therefore, the power dissipated by the resistor increases by approximately 6.09% when the current increases by 3%.
The power (P) dissipated by a resistor is given by the formula:
P=I2R
where I is the current through the resistor and R is the resistance.
We are given that the current increases by 3%. This can be expressed as:
ΔI=0.03I
where ΔI is the change in current.
The new current I′ after the increase can be written as:
I′=I+ΔI=I+0.03I=1.03I
The new power P′ after the increase in current can be calculated using the new current:
P′=(I′)2R=(1.03I)2R=1.0609I2R
The original power P is:
P=I2R
The change in power ΔP is:
ΔP=P′−P=(1.0609I2R)−(I2R)=0.0609I2R
The percentage change in power can be calculated as:
Percentage Change in Power=(ΔPP)×100=(0.0609I2RI2R)×100=6.09%
Therefore, the power dissipated by the resistor increases by approximately 6.09% when the current increases by 3%.
Topper's Solved these Questions
- QUESTION PAPER 2013BOOK - KVPY PREVIOUS YEARCHAPTER - QUESTION PAPER 2013EXERCISE - PART-II (PHYSICS)
5 Videos
- QUESTION PAPER 2013BOOK - KVPY PREVIOUS YEARCHAPTER - QUESTION PAPER 2013EXERCISE - PART-I ( PHYSICS)
20 Videos
- MOCK TEST 9BOOK - KVPY PREVIOUS YEARCHAPTER - MOCK TEST 9EXERCISE - EXERCISE
19 Videos
- QUESTION PAPER 2020BOOK - KVPY PREVIOUS YEARCHAPTER - QUESTION PAPER 2020EXERCISE - PART-I : PHYSICS
50 Videos
Similar Questions
Knowledge Check
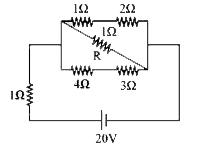
The power dissipated 6Ω resistor is
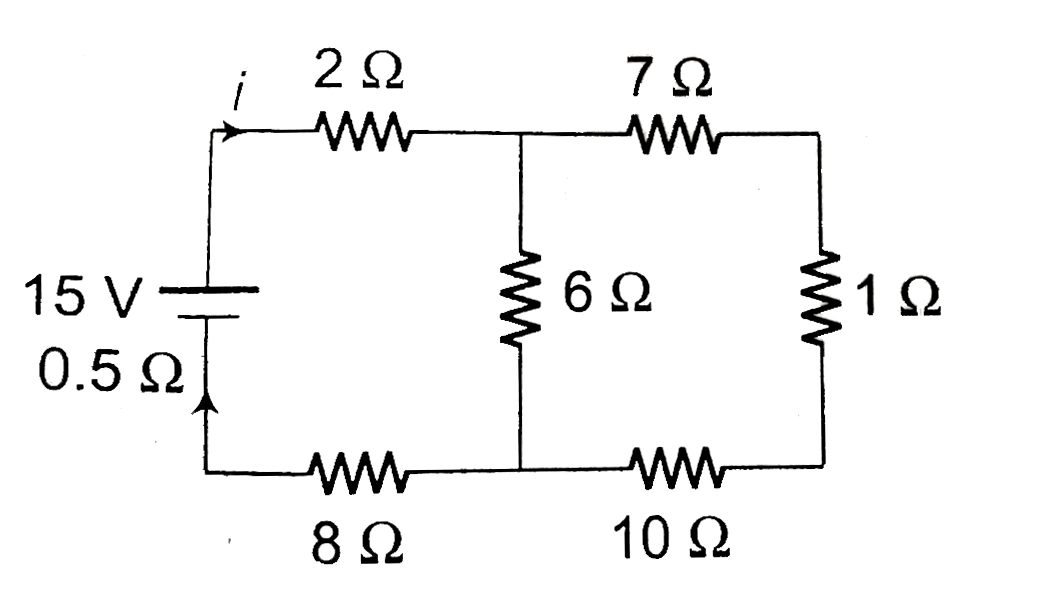 A278WB916WC616WD316W
A278WB916WC616WD316WFind the current through resistor R.
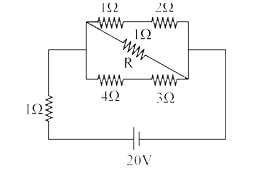 A9AB10AC11AD8A
A9AB10AC11AD8AIf the current through a resistor is increased by 50%, the increase in power dissipated will be (assume the temperature remains constant)
A2.25B2C2.5D1.25
Find the current through 4Ω resistor in the circuit shown in figure.
View Solution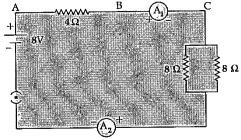
Power dissipated in 4Ω resistor is :
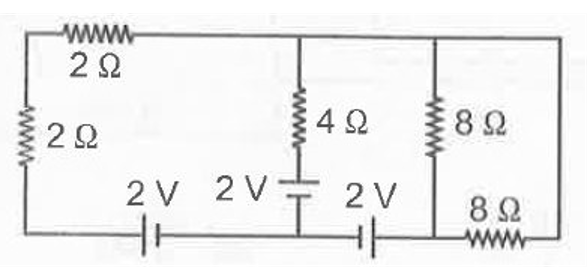
View SolutionCurrent through the 5Ω resistor is
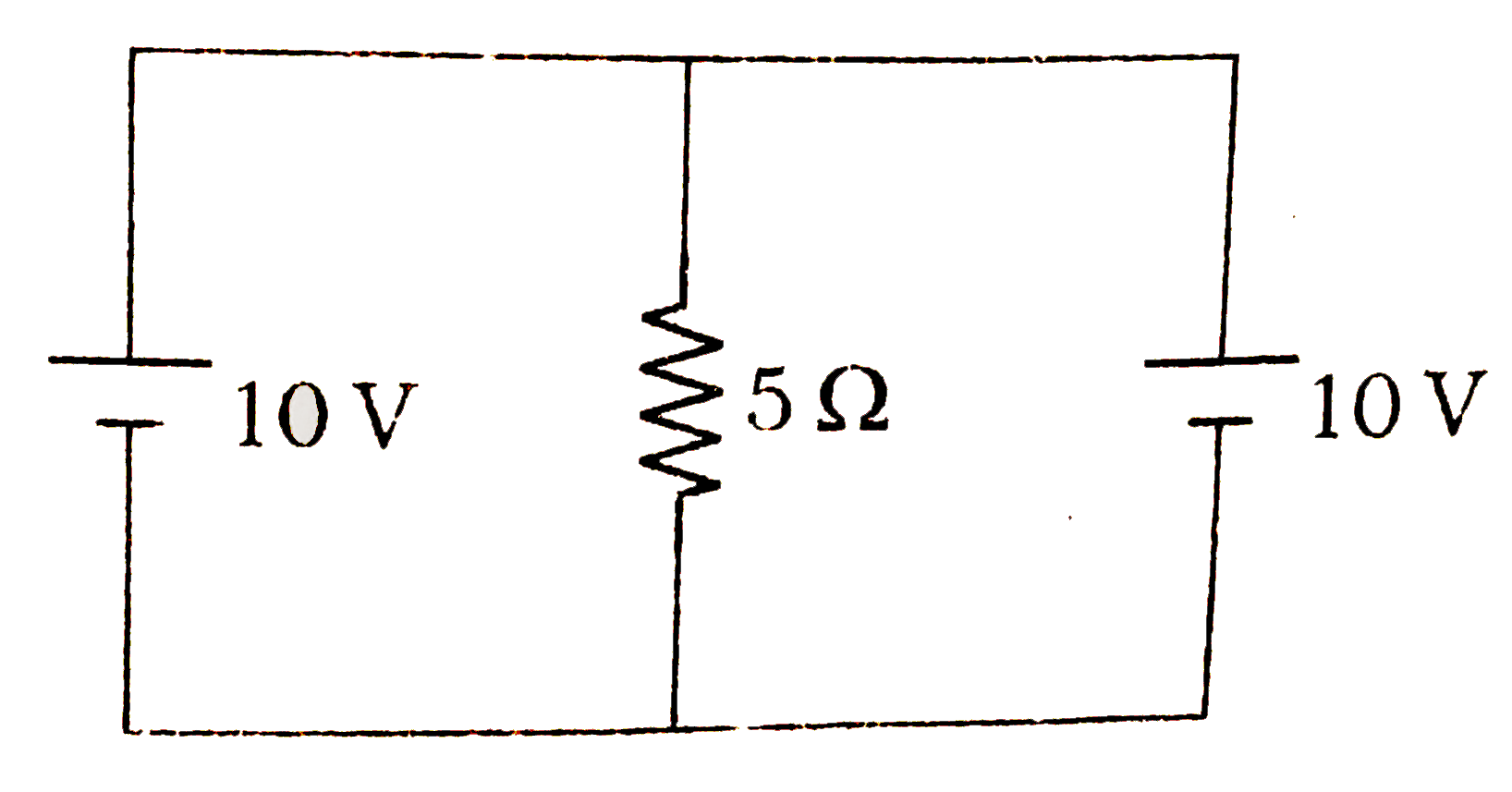
View SolutionA current of 3A flows through the 2Ω resistor shown in the circuit the power dissipated in the 5Ω resistor is
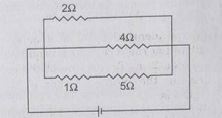
View SolutionA current of 3A flows through the 2Ω resistor shown in the circuit the power dissipated in the 5Ω resistor is

View Solution