(a) Deduce an expression for the frequency of revolution of a charged particle in a magnetic field and show that it is independent of velocity or energy of the particle.
(b) Draw a schematic sketch of a cyclotron. Explain, giving the essential details of its construction, how it si used to accelerate the charged particles.

Text Solution

Verified by Experts

(a) When a charged particle with charge q moves inside a magnetic field $\to β$ with velocity v, it experiences a force, which is given by : $\to F = q ({\to v}^{\times} \to β)$
Here $\to v$ is perpendicular to $\to β$ , $\to F$ is the force on the charged particle which acts as the centipetal force and makes it move along a circular path.

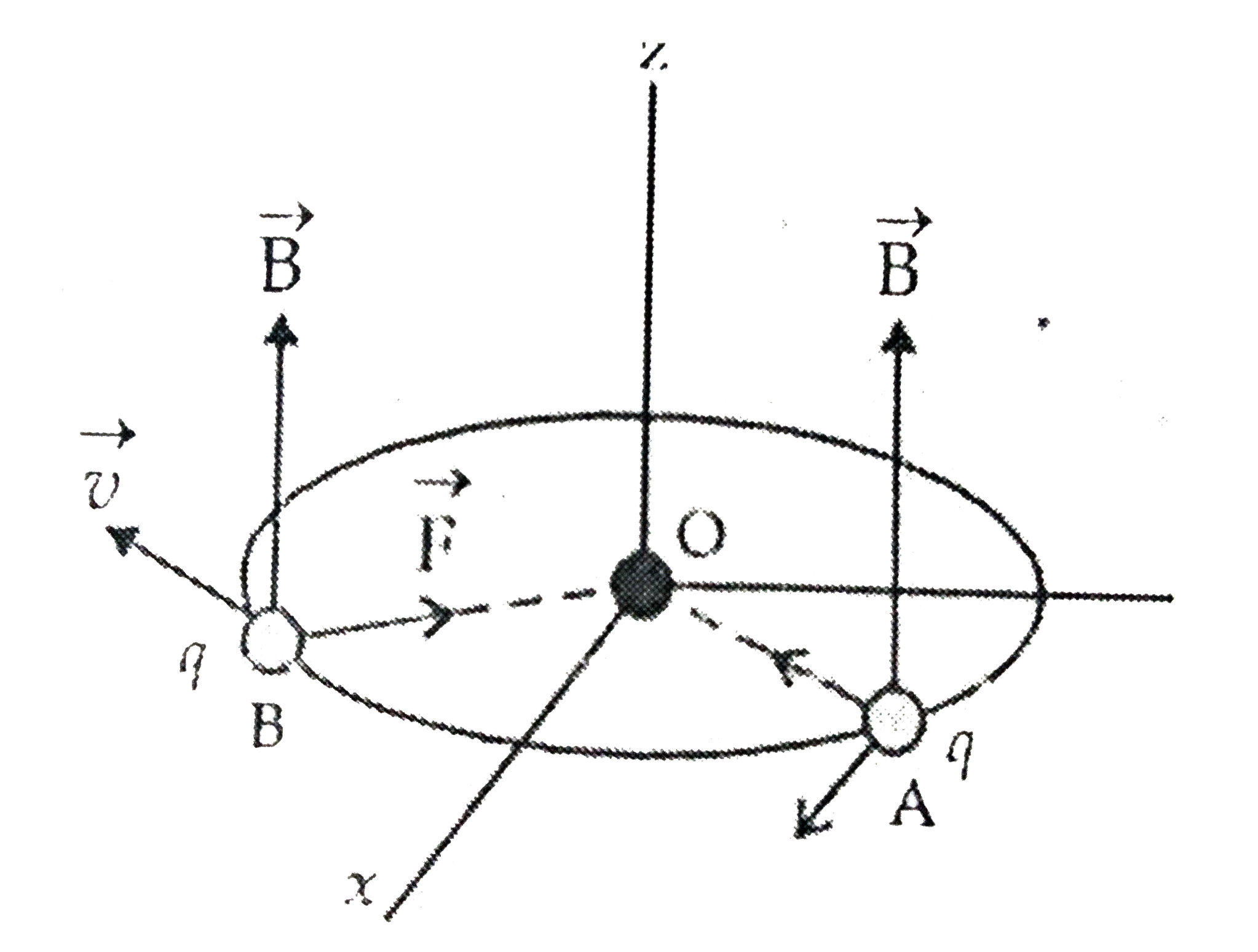
Let m be the mass of the charged particle and r be the radius of the circular path.
$∴ q ({\to v}^{\times} \to β) = m v^{2}$
V and B are at right angles.
$∴ q v B = \frac{m v^{2}}{r} ∴ \frac{m v}{B q}$
Time period of circular motion of the charged particle can be calculated as shown below :
$T = \frac{2 π r}{v} = \frac{2 π}{v} \frac{m v}{B q} \Rightarrow T = \frac{2 π m}{B q}$
$∴ Angular frequency is ω = \frac{2 π}{T} ∴ ω = \frac{B q}{m}$ .
Therefore, the frequency of the revolution of the charged particle is independent of velocity or energy of the particle.
(b) Cyclotron :

Updated on:21/07/2023

|

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

When a charged particle enters a uniform magnetic field its kinetic energy
Aremains constant
Bincreased
Cdecreases
Dbecomes
When a charged particle enters a uniform magnetic field its kinetic energy
ARemains constant
BIncreases
CDecreases
DBecomes zero

XII BOARDS PREVIOUS YEAR-XII BOARDS-SET-I

Home
Ask Doubt
Profile