State Gauss's law in electrostatics. Derive an expression for the electric field due to an infinitely long straight uniformly charged wire.

Text Solution

Verified by Experts

The total electric flux $(φ)$ through any closed surface s in free space to $\frac{1}{\in_{0}}$ times the total electric charge q enclosed by the surface.
$φ = \oint s \to E . d \to s = q / \in_{0}$
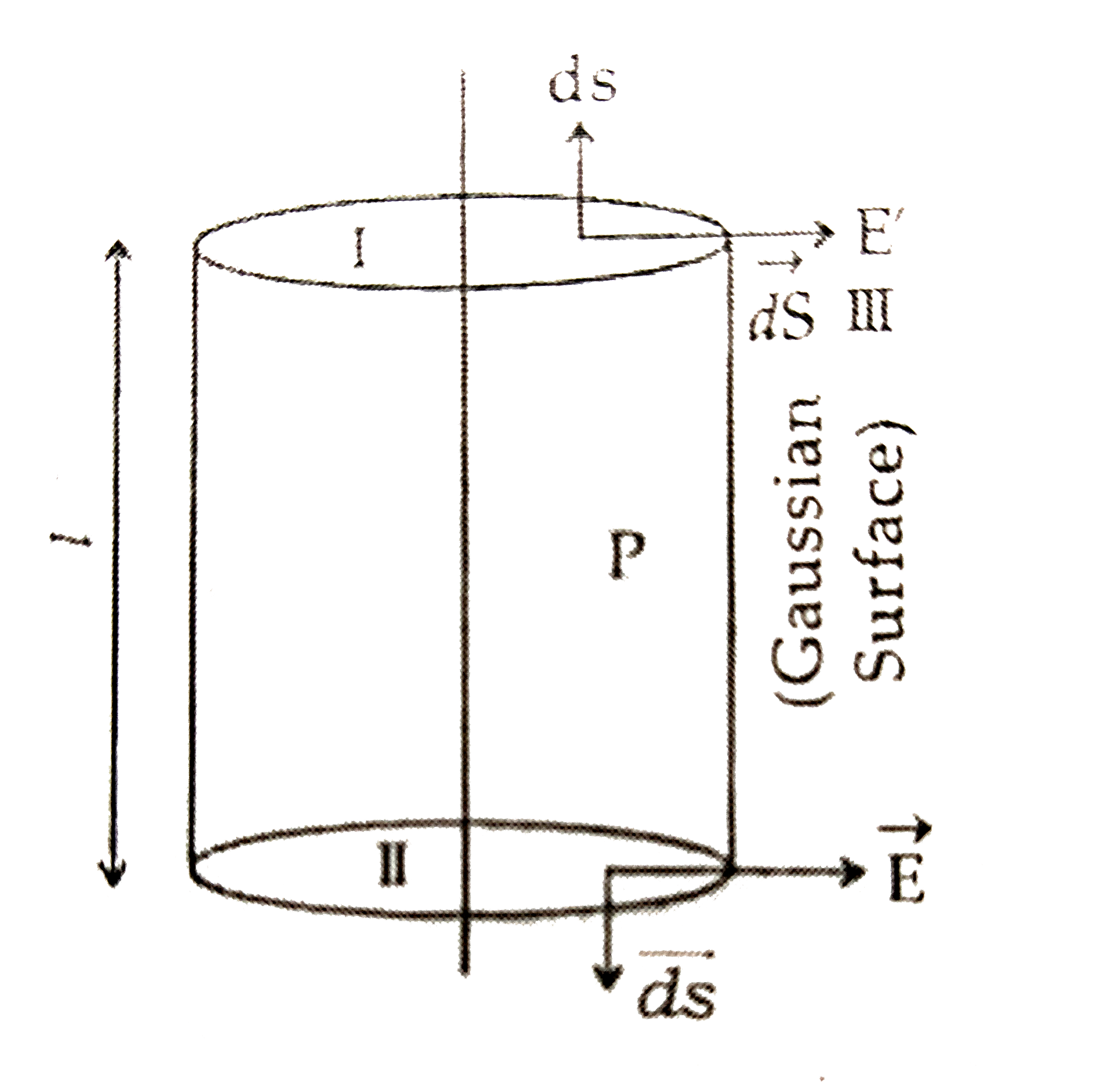
Take a thin long wire ( $l = α$ ) with linear charge density $λ$ symmetric about the axis of the wire . At P, $\to E$ is to calculated, draw an imaginary cylinder (Gaussian Surface) at distance r from the line.
Charged enclosed = $q = λ l$ from Gauss'a theorem $\oint s \to E . d \to S = \frac{q}{\in_{0}} = \frac{λ l}{\in_{0}} .$
Top face (I) Bottom face II and curved face III ar the segments of Gaussian surface. So $\frac{λ l}{\in_{0}} = \oint s \to E . d \to S = \int I \to E . d \to S + \int I I \to E . d \to S + \int I I I \to E . d \to S$
In I and II angle between $\to E and d \to S is 90^{\circ} so, {cos 90}^{\circ} = 0 so, \to E . d \to S$ for both the region is zero.
Electric flux will cross through only curved surface and now $\oint I I I \to E . d \to S = \frac{λ l}{\in_{0}} \Rightarrow \int I I I \to E d s cos 0 = \frac{λ l}{\in_{0}}$
$\int I I I \to E . d \to S = \frac{λ l}{\in_{0}}$
But $\int d s = 2 π r l = C S A = of cylinder$
$\Rightarrow E \times 2 π r l = \frac{λ l}{\in_{0}} \Rightarrow E = \frac{λ}{2 π \in_{0} r}$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

XII BOARDS PREVIOUS YEAR-XII BOARDS-SECTION-C

Home
Ask Doubt
Profile