A particle is at x =+ 5 m at t =0,x =- 7 m at t = 6 s and x = + 2 at t = 10s. Find the average velocity of the particle during the intervals
(a)t=0 to t=6s
(b)t=6s to 6=10s
(c ) t=0 to t=10s . Solution in Telugu
From the definition of average velocity
x=ΔxΔt=x2−x1t2−t1
(a)The average velocity between the times t=0 to t= 6s
x1=+5m,t1=0,x2=−7 m t2=6s
Hence v1=x2−x1t2−t1=−7−56−0=−2ms−1
(b)The average velocity between the times
t2=6s to t3=10 s is
v2=x3−x2t3−t2=2−(−7)10−6=94=2.25ms−1
(c)The average velocity between times t1=0 to t3=10 s is
v3=x3−x1t3−t1=2−510−0=−0.3ms−1
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE Book:AAKASH SERIESChapter:MOTION IN A STRAIGHT LINE Exercise:EXERCISE -I
Explore 58 Videos
- MOTION IN A STRAIGHT LINE Book:AAKASH SERIESChapter:MOTION IN A STRAIGHT LINE Exercise:EXERCISE -II
Explore 80 Videos
- MOTION IN A PLANEBook:AAKASH SERIESChapter:MOTION IN A PLANEExercise:QUESTION FOR DESCRIPTIVE ANSWER
Explore 7 Videos
- MOVING CHARGES AND MAGNETISMBook:AAKASH SERIESChapter:MOVING CHARGES AND MAGNETISMExercise:EXERCISE-III
Explore 45 Videos
Similar Questions
The ratio of the numerical values of the average velocity and average speed of a body is always
View SolutionA person travels along a straight road for half the distance with velocity V1 and the remaining half distance with velocity V2 the average velocity is given by
View SolutionA particle is projected over a triangle from one end of a horizontal base and garzing the vertex falls on the other end of the base . If α and β the base angles and θ the angle of projection then show that tanθ=tanα+tanβ.
View SolutionA proton, a deuteron and an a particle having same momentum enter a uniform magnetic field at right angles to the field. Then the ratio of their angular momenta during their motion in the magnetic field is
View SolutionFigure shows x-t graph of a particle. Find the Time T Such that the Average Velocity of the Particle During the Period 0 to T is Zero..
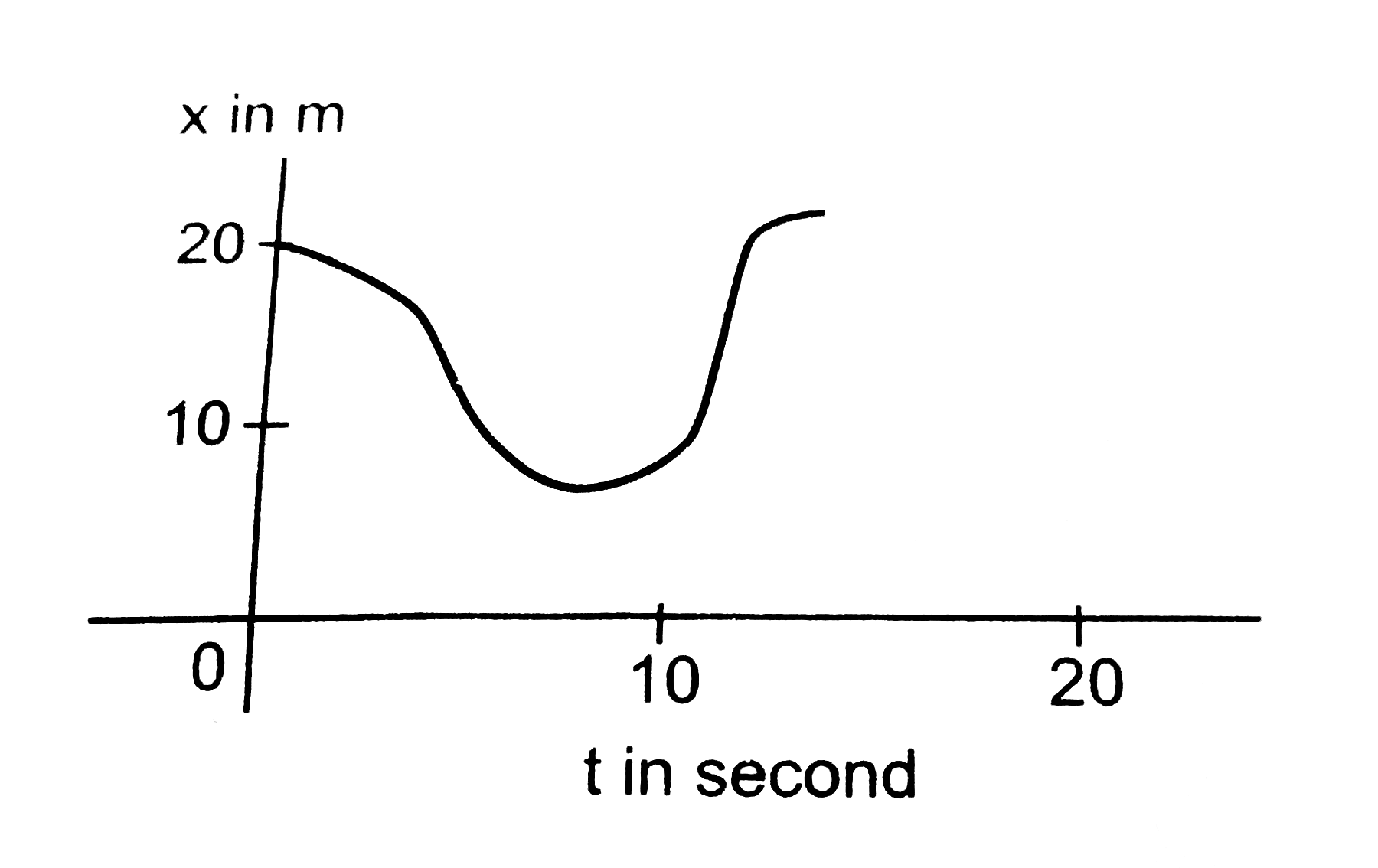
View SolutionVelocity (in m/s) of a particle moving along x-axis varies with time as, v= (10+ 5t -t^2) At time t=0, x=0. Find (a) acceleration of particle at t = 2 s and (b) x-coordinate of particle at t=3s
View SolutionA particle is moving along the x-axis such that s=6t-t^(2) , where s in meters and t is in second. Find the displacement and distance traveled by the particle during time interval t=0 to t=5 s .
View SolutionThe position of a particle moving on the x-axis is given by x=t^(3)+4t^(2)-2t+5 where x is in meter and t is in seconds (i) the velocity of the particle at t=4 s is 78 m//s (ii) the acceleration of the particle at t=4 s is 32 m//s^(2) (iii) the average velocity during the interval t=0 to t=4 s is 30 m//s (iv) the average acceleration during the interval t=0 to t=4 s is 20 m//s^(2)
View SolutionA particle is moving along positive x direction and experiences a constant acceleration of 4m/s2 in negative x direction. At time t=3 second its velocity was observed to be 10m/s in positive x direction.
(a) Find the distance travelled by the particle in the interval t=0 to t=3s. Also find distance travelled in the interval t=0 to t=7.5s..
(b) Plot the displacement – time graph for the interval t=0 to 7.5s.
View SolutionSuppose that a particle mvoes on a straight line so that is velocity at time t is v(t)=(t^(2)-2t)m//s . (a). Find the displacement of the particle during the time interval 0 le t le 3 (b). Find the distance traveled by the particle during the time interval 0 le t le 3 .
View SolutionThe position of a particle moving on X-axis is given by x=At2+Bt+C The numerical values of A, B and C are 7, -2 and 5 respectively and SI units are used. Find
(a) The velocity of the particle at t= 5
(b) The acceleration of the particle at t =5
(c ) The average velocity during the interval t = 0 to t = 5
(d) The average acceleration during the interval t = 0 to t = 5
View SolutionThe position of a particle varies with time according to the relation x=3t2+5t3+7t, where x is in m and t is in s. Find
(i) Displacement during time interval t = 1 s to t = 3 s.
(ii) Average velocity during time interval 0 - 5 s.
(iii) Instantaneous velocity at t = 0 and t = 5 s.
(iv) Average acceleration during time interval 0 - 5 s.
(v) Acceleration at t = 0 and t = 5 s.
View Solutionएक कण का वेग समय ग्राफ चित्र में प्रदर्शित है। ज्ञात कीजिए।
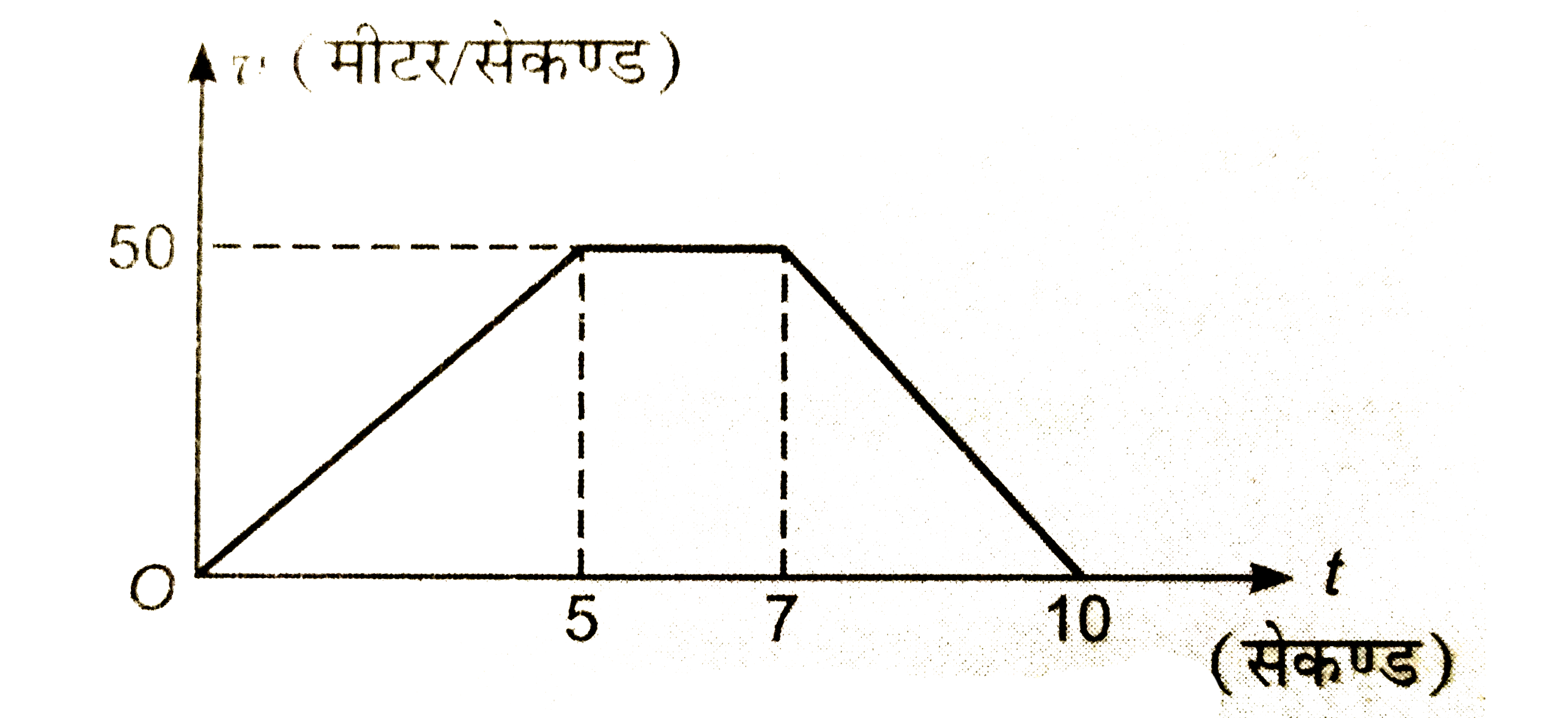
(i) t=0 से t=5 सेकण्ड के समयान्तराल में कण का त्वरण।
(ii) t=5 से t=7 सेकण्ड के समयान्तराल में कण का त्वरण।
(iii) t=7 से t=10 सेकण्ड के समयान्तराल में कण का त्वरण।
(iv) t=0 से t=7 सेकण्ड के समयान्तराल में कण द्वारा तय दूरी।
(v) t=0 से t=10 सेकण्ड के समयान्तराल में कण द्वारा तय दूरी।
View Solutionx -अक्ष पर चलते हुए एक कण का स्थान x=At3+Bt2+Ct+D के अनुसार बदलता है | SI इकाइयों में A, B, C एवं D के सांख्यिक मान क्रमशः 1,4,−2 तथा 5 है | (a) A, B, C तथा D के विमीय - सूत्र निकले | (b) समय t=4s पर कण का वेग निकालें | (c) t=4s पर कण का त्वरण निकालें | (d ) t=0 से t=4s के अंतराल में कण का औसत वेग निकाले | (e) t = 0 से t = 4s के अंतराल में कण का औसत त्वरण निकालें |
View Solutionचित्र में x - अक्ष पर चलते हुए एक कण का x - निर्देशांक समय के फलां के रूप में दिखाया गया है | ज्ञात करे, (a) t = 0 से t = 10s के अंतराल में औसत वेग (b) 2, 5, 8 तथा 12 s पर कण के वेग |
View SolutionAcceleration of a particle is increasing linearly with time. Its acceleration is 10 m//s^(2) at t =0 and 20 m//s^(2) at t = 5s. "Also" , its speed is 5m/s at t =0 and its positions is x= -100m at t =0 .Find at time t its acceleration ,velocity and positions.
View Solution
