A circular coil of radius R carries a curretn. Find an expression for the magnetic field due to this coil at its centre. Also find the direction of field.

Text Solution

Verified by Experts

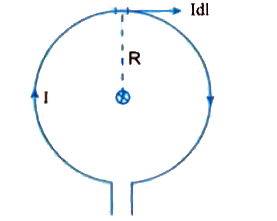
Consider a circular loop of radius R carrying a current I in clockwise direction. The loop may be considered to be divided into a large number of current elements.
Consider one such current element of length dl as shown in fig. Magnetic field at the centre point O of the loop due to this element, as per Bio-Sarvart.s law is
$d B = \frac{μ_{0}}{4 π} \cdot \frac{I d l {sin 90}^{\circ}}{R^{2}} = \frac{μ_{0}}{4 π} \cdot \frac{I d l}{R^{2}} [ Here = θ = 90^{\circ}]$
The total magnetic field due to current loop
$B = \frac{μ_{0}}{4 π} \cdot \frac{I}{R^{2}} \sum d l = \frac{μ_{0} I}{4 π R^{2}} \cdot (2 π R) = \frac{μ_{0} I}{2 R} [∴ \sum d l = 2 π R]$
If instead of a single loop we have a circular coil of N turns, then
$B = \frac{μ_{0} N I}{2 R}$
The magnetic field is directed perpendicular to the plane of paper directed inward.

Updated on:21/07/2023

A circular coil of radius R carries an electric current. The magnetic field due to the coil at a point on the axis of the coil located at a distance r from the centre of the coil, such that $r > > R$ , varies as
A $\frac{1}{r}$
B $\frac{1}{r^{3 / 2}}$
C $\frac{1}{r^{2}}$
D $\frac{1}{r^{3}}$
A circular coil of radius $R$ carries an electric current. The magnetic field due to the coil at a point on the axis of the coil located at a distance $r$ from the centre of the coil, such that $r > > R$ , varies as
A $\frac{1}{r}$
B $\frac{1}{r^{3}}$
C $\frac{1}{r^{2}}$
D $\frac{1}{r^{3 / 2}}$
A circular coil of radius $R$ carriers an electric current. The magnetic field due to the coil at a point on the axis of the coil located at a distance $r$ from the centre of the coil, such that $r > > R$ , varries as
A $\frac{1}{r}$
B $\frac{1}{r^{3 / 2}}$
C $\frac{1}{r^{2}}$
D $\frac{1}{r^{3}}$