Explain how Biot-Savart's law enables one to express the Ampere's circuital law in the integral form , viz.,
∮→B.→dl=μ0I
where I is the total current passing through the surface.
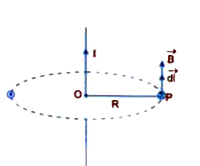
Let us consider an infinitely long straight wire in which a current I is flowing. To find magnetic field at a point P situated at a normal distance R from the wire consider a circular loop of radius R around the wire and in a plane perpendicular to the wire so that magnetic field →B is tangential to the circumerence of the circle. For such a case
∮→B.→dl=∫Bdl=B∫dl=B.2πR
But as per Biot-Savart.s law we know that magnetic field B at a normal distance R from a long long straight current carrying wire is
B=μ0I2πR
Hence, we get :
∮→B.→dl=(μ0I2πR)2πR=μ0I.
which is the integral form of Ampere.s circuital law.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISM BOOK - U-LIKE SERIESCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - LONG ANSWER QUESTIONS-I
33 Videos
- MOVING CHARGES AND MAGNETISM BOOK - U-LIKE SERIESCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - LONG ANSWER QUESTIONS-II
11 Videos
- MOVING CHARGES AND MAGNETISM BOOK - U-LIKE SERIESCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - VERY SHORT ANSWER QUESTIONS
39 Videos
- MODEL TEST PAPER 3 (UNSOLVED)BOOK - U-LIKE SERIESCHAPTER - MODEL TEST PAPER 3 (UNSOLVED)EXERCISE - SECTION A
3 Videos
- NUCLEIBOOK - U-LIKE SERIESCHAPTER - NUCLEIEXERCISE - Self Assessment Test
10 Videos
Similar Questions
Read the following passage and then answer questions (a) to (d) on the basis of your under- standing of the passage and the related studied concepts.
We are familiar with Ampere.s circuital law which states that for an open surface with a boundary around a current the line integral of magnetic field around the entire boundary of an open surface is equal to μ0 times the total current passing through the surface i.e.
∮→B.→dl=μ0I
Later on, Maxwell showed that for logical consistency, a changing electric field must also produce a magnetic field. In this context Maxwell introduced the concept of a displacement current given as per relation
ID=∈0dϕEdt
Thus, as per generalisation made by Maxwell, the source of a magnetic field is not just the conduction electric current due to following charges but also the time rate of change of electric field. In this way, Maxwell modified Ampere.s circuital law and in its modified the law is expressed as:
∮→B.→dl=μ0[IC+ID]=μ0[IC+∈0dϕEdt]
In all respects, the displacement current has the same physical effects as the conduction current. It is observed that in same cases, e.g., steady electric field in a wire, displacement current may be zero. In other cases, e.g., a capacitor being charged, both conduction and displacement currents may be present in different regions of space. In most of the cases, conduction current and displacement current may be present simultaneously in the same region of space because there exist no perfectly conducting or perfectly insulating medium. Moreover, there may be large regions of space where there is no conduction current but there is only a displacement current due to time varying electric field.
What did Maxwell suggest to make Ampere.s circuital law logical consistent?
View SolutionRead the following passage and then answer questions (a) to (d) on the basis of your under- standing of the passage and the related studied concepts.
We are familiar with Ampere.s circuital law which states that for an open surface with a boundary around a current the line integral of magnetic field around the entire boundary of an open surface is equal to μ0 times the total current passing through the surface i.e.
∮→B.→dl=μ0I
Later on, Maxwell showed that for logical consistency, a changing electric field must also produce a magnetic field. In this context Maxwell introduced the concept of a displacement current given as per relation
ID=∈0dϕEdt
Thus, as per generalisation made by Maxwell, the source of a magnetic field is not just the conduction electric current due to following charges but also the time rate of change of electric field. In this way, Maxwell modified Ampere.s circuital law and in its modified the law is expressed as:
∮→B.→dl=μ0[IC+ID]=μ0[IC+∈0dϕEdt]
In all respects, the displacement current has the same physical effects as the conduction current. It is observed that in same cases, e.g., steady electric field in a wire, displacement current may be zero. In other cases, e.g., a capacitor being charged, both conduction and displacement currents may be present in different regions of space. In most of the cases, conduction current and displacement current may be present simultaneously in the same region of space because there exist no perfectly conducting or perfectly insulating medium. Moreover, there may be large regions of space where there is no conduction current but there is only a displacement current due to time varying electric field.
In how many ways a magnetic field produced in free space without the presence of permanent magnet?
View Solution
Knowledge Check
Statement I: no electric current will be present within a region having uniform and constant magetic field.
Statement II: Within a region of unifrom and cinstant magnetic field →B, the path integral of magnetic field ∮→B.d→l along any closed path is zero. Hence, from Ampere cirauital law ∮→B.d→l=μ0I (where the given terms ahve usual meaning), no current can be present within a region having uniform and constant magnetic field .A(a) Statement I is True, Statement II is True, Statement II is correct expaination for Statement I.B(b) Statement I is True, Statement II is True, Statement II is NOT a correct expaination for Statement I.C( c) Statement I is True, Statement II is false.D( d) Statement I is False, Statement II is True.
Read the following passage and then answer questions (a) to (d) on the basis of your under- standing of the passage and the related studied concepts.
We are familiar with Ampere.s circuital law which states that for an open surface with a boundary around a current the line integral of magnetic field around the entire boundary of an open surface is equal to μ0 times the total current passing through the surface i.e.
∮→B.→dl=μ0I
Later on, Maxwell showed that for logical consistency, a changing electric field must also produce a magnetic field. In this context Maxwell introduced the concept of a displacement current given as per relation
ID=∈0dϕEdt
Thus, as per generalisation made by Maxwell, the source of a magnetic field is not just the conduction electric current due to following charges but also the time rate of change of electric field. In this way, Maxwell modified Ampere.s circuital law and in its modified the law is expressed as:
∮→B.→dl=μ0[IC+ID]=μ0[IC+∈0dϕEdt]
In all respects, the displacement current has the same physical effects as the conduction current. It is observed that in same cases, e.g., steady electric field in a wire, displacement current may be zero. In other cases, e.g., a capacitor being charged, both conduction and displacement currents may be present in different regions of space. In most of the cases, conduction current and displacement current may be present simultaneously in the same region of space because there exist no perfectly conducting or perfectly insulating medium. Moreover, there may be large regions of space where there is no conduction current but there is only a displacement current due to time varying electric field.
Does displacement current need a conductor to flow.
View SolutionRead the following passage and then answer questions (a) to (d) on the basis of your under- standing of the passage and the related studied concepts.
We are familiar with Ampere.s circuital law which states that for an open surface with a boundary around a current the line integral of magnetic field around the entire boundary of an open surface is equal to μ0 times the total current passing through the surface i.e.
∮→B.→dl=μ0I
Later on, Maxwell showed that for logical consistency, a changing electric field must also produce a magnetic field. In this context Maxwell introduced the concept of a displacement current given as per relation
ID=∈0dϕEdt
Thus, as per generalisation made by Maxwell, the source of a magnetic field is not just the conduction electric current due to following charges but also the time rate of change of electric field. In this way, Maxwell modified Ampere.s circuital law and in its modified the law is expressed as:
∮→B.→dl=μ0[IC+ID]=μ0[IC+∈0dϕEdt]
In all respects, the displacement current has the same physical effects as the conduction current. It is observed that in same cases, e.g., steady electric field in a wire, displacement current may be zero. In other cases, e.g., a capacitor being charged, both conduction and displacement currents may be present in different regions of space. In most of the cases, conduction current and displacement current may be present simultaneously in the same region of space because there exist no perfectly conducting or perfectly insulating medium. Moreover, there may be large regions of space where there is no conduction current but there is only a displacement current due to time varying electric field.
Define displacement current.
View Solution(a) Using Biot-Savart's law, derive the expression for the magnetic field in the vector form at a point on the axis of a circular current loop.
(b) What does a toroid consist of? Find out the expression for the magnetic field inside a toroid for N turns of the coil having the average radius r and carrying a current I. Show the magnetic field in the open space inside and exterior to the toroid is Zero.
View SolutionStatement I: no electric current will be present within a region having uniform and constant magetic field.
Statement II: Within a region of unifrom and cinstant magnetic field →B, the path integral of magnetic field ∮→B.d→l along any closed path is zero. Hence, from Ampere cirauital law ∮→B.d→l=μ0I (where the given terms ahve usual meaning), no current can be present within a region having uniform and constant magnetic field .
View SolutionYou know that Ampere's circuital law is mathematically expressed as given below.
∮→B→dt−μ0I
Also you know that this law was corrected by Maxwell and which is known as Ampere-Maxwell law. Write the general form of the law and name the additional term.
View SolutionStatement (A) : Ampere's law states that the line integral of →B.→dl along a closed path round the current carrying conductor is equal to μ0i (i is the net current through the surface bounded by the closed path)
Statement (B) : Ampere's law can be derived from Biot savart's law
View Solutionwrite the expression for the generalized form of Ampere's circuital law. Discuss its significance and describe briefly how the concept of dislacement current is explained through charing/discharging of a capacitor in an electric circuit.
View Solution
