Magnetic Field due to Circular Coil
To solve the problem of finding the magnetic field due to a circular coil at a point along its axis, we can follow these steps:
1. Understand the Setup:
- We have a circular coil of radius r carrying a current I.
- We want to find the magnetic field B at a point P located at a distance z along the axis of the coil.
2. Use the Biot-Savart Law:
- The magnetic field dB due to a small segment of the coil dl is given by the Biot-Savart Law:
dB=μ04πIdl×^rr2
- Here, ^r is the unit vector pointing from the current element to the point P, and r is the distance from the current element to the point P.
3. Determine the Geometry:
- For a circular coil, the distance r from the current element to point P can be expressed as:
r=√z2+R2
- Where R is the radius of the coil.
4. Integrate Over the Coil:
- The total magnetic field B at point P is obtained by integrating dB around the entire coil:
B=∫dB
- Due to symmetry, only the component along the axis (the z-direction) will contribute to the total magnetic field.
5. Calculate the Magnetic Field:
- The expression for the magnetic field at point P becomes:
Bz=μ0I4π∫dl(z2+R2)3/2
- The integral of dl over the entire coil gives 2πR:
Bz=μ0I4π⋅2πR(z2+R2)3/2
- Simplifying this gives:
Bz=μ0IR2(z2+R2)3/2
6. Special Case at the Center of the Coil:
- When z=0 (the center of the coil), the magnetic field simplifies to:
B=μ0I2R
Final Answer:
The magnetic field at a distance z along the axis of a circular coil is given by:
Bz=μ0IR2(z2+R2)3/2
At the center of the coil (z=0):
B=μ0I2R
- We have a circular coil of radius r carrying a current I.
- We want to find the magnetic field B at a point P located at a distance z along the axis of the coil.
- The magnetic field dB due to a small segment of the coil dl is given by the Biot-Savart Law:
dB=μ04πIdl×^rr2
- Here, ^r is the unit vector pointing from the current element to the point P, and r is the distance from the current element to the point P.
- For a circular coil, the distance r from the current element to point P can be expressed as:
r=√z2+R2
- Where R is the radius of the coil.
- The total magnetic field B at point P is obtained by integrating dB around the entire coil:
B=∫dB
- Due to symmetry, only the component along the axis (the z-direction) will contribute to the total magnetic field.
- The expression for the magnetic field at point P becomes:
Bz=μ0I4π∫dl(z2+R2)3/2
- The integral of dl over the entire coil gives 2πR:
Bz=μ0I4π⋅2πR(z2+R2)3/2
- Simplifying this gives:
Bz=μ0IR2(z2+R2)3/2
- When z=0 (the center of the coil), the magnetic field simplifies to:
B=μ0I2R
The magnetic field at a distance z along the axis of a circular coil is given by:
Bz=μ0IR2(z2+R2)3/2
At the center of the coil (z=0):
B=μ0I2R
Topper's Solved these Questions
Similar Questions
State Biot-Savart law, giving the mathematical expression for it.
Use this law to derive the expression for the magnetic field due to a circular coil carrying current at a point along its axis.
How does a circular loop carrying curent behave as a magnet?
View Solution(a) State Biot - Savart law and ecpress it in the vector form.
(b) Using Biot - Savart law, law obtain the expression for the magnetic field due to a circular coil of radius r, carrying a current I at point on its axis distant x from the centre of the coil.
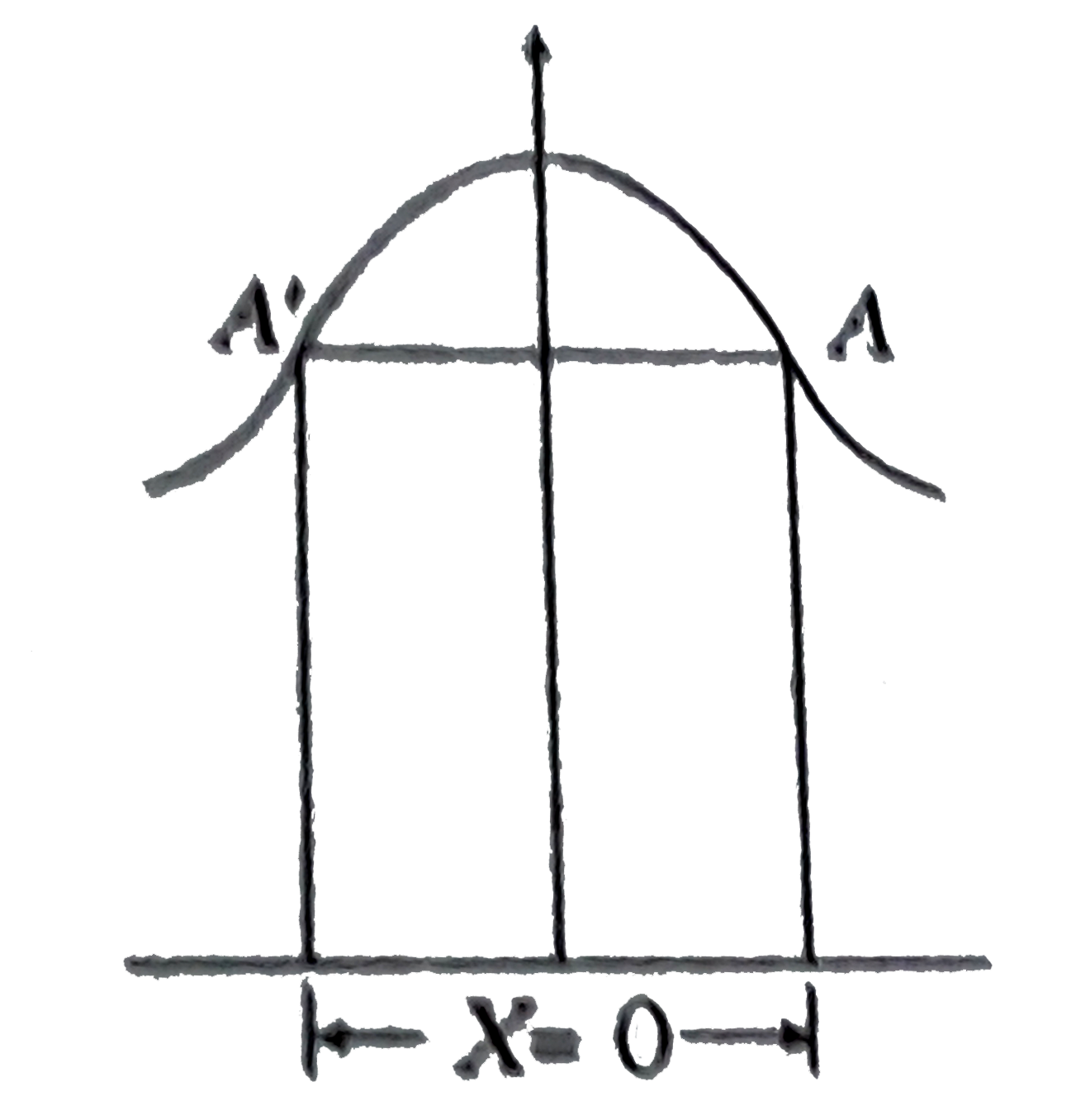
View SolutionThe variation of magnetic field (B) due to circular coil as the distance X varies is shown in the graph. Which of the following is false
View SolutionAssertion A charged particle is rotating in a circular path in uniform magnetic field. Then, plane of circle is perpendicular to the magnetic field.
Reason Circular motion is a two-dimensional motion.
View SolutionDraw the pattern of magnetic field lines for a circular coil carrying current.
View SolutionThe magnetic field due to current carrying circular coil loop of radius 6 cm at a point on axis at a distance of 8 cm from the centre is 54μT . What is the value at the centre of loop ?
View SolutionMagnetic field due to 0.1A current flowing through a circular coil of radius 0.1m and 1000 turns at the centre of the coil is
View SolutionA circular coil of radius R carries an electric current. The magnetic field due to the coil at a point on the axis of the coil located at a distance r from the centre of the coil, such that r>>R, varies as
View SolutionA circular coil of radius R carries an electric current. The magnetic field due to the coil at a point on the axis of the coil located at a distance r from the centre of the coil, such that r>>R, varies as
View SolutionTwo similar coils are kept mutually perpendicular such that their centres coincide. At the centre, find the ratio of the magnetic field due to one coil and the resultant magnetic field by both coils, if the same current is flown
View Solution
