Two capacitors of capacitances C1 and C2 are connected in parallel. If a charge Q is given to the combination, the ratio of the charge on the capacitor C1 to the charge on C2 will be
C1C2
√C1C2
√C2C1
C2C1
The correct Answer is:A
(a) C1C2
[Hint: When two capacitors are connected in parallel, potential difference across them is same i.e., V1=V2=V(say), So Q1Q2=C1V1C2V2=C1VC2V=C1C2.]
Topper's Solved these Questions
- EXAMINATION PAPER 2020 (SOLVED)BOOK - U-LIKE SERIESCHAPTER - EXAMINATION PAPER 2020 (SOLVED)EXERCISE - SECTION B
9 Videos
- EXAMINATION PAPER 2020 (SOLVED)BOOK - U-LIKE SERIESCHAPTER - EXAMINATION PAPER 2020 (SOLVED)EXERCISE - SECTION C
8 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SELF ASSESSMENT TEST
1 Videos
- MAGNETISM AND MATTERBOOK - U-LIKE SERIESCHAPTER - MAGNETISM AND MATTEREXERCISE - SELF ASSESSMENT TEST (Section D)
1 Videos
Similar Questions
Knowledge Check
Two capacitors of capacitances C1andC2 are connected in parallel. If a charge q is given to the assembly, the charge gets shared. The ratio of the charge on the capacitor C1 to the charge on C2 is
AC1C2BC2C1CC1C2D1C1C2Condsider
 .
.
The charge on capacitor C1 is.A225μCB135μCC270μCD360μCA capacitor of capacitance C is given charge Q and then connected in parallel to a coil of inductance L. There is no resitance in the circuit. When the charge on the capacitor becomes zero, the current in the coil will be
AQ√LCBQ√LCCQ√CLDzero
Two capacitors of capacitance C1 and C2 are connected in parallel and a charge Q is delivered to the combination. The two are then disconnected and reconnected in series. What are the new potential differences and charge on the capacitors?
View SolutionTwo capacitors of capacitances C_1 and C2 are connected in parallel across a battery. IfQ1 and Q2 respectively be the charges on the capacitors, then Q1Q2 will be equal to
View SolutionTwo capacitors of capacitances C1=2μF and C2=8μF are connected in series and the resulting combination is connected across a 300V battery. Calculate the charge, potential difference and energy stored in the capacitor separately.
View SolutionTwo capacitors of capacitances C1=2μF and C2=8μF are connected in series and the resulting combination is connected across a 300V battery. Calculate the charge, potential difference and energy stored in the capacitor separately.
View SolutionTwo capacitors C1 and C2 are connected to a battery of 6V as shown in Fig. Find the charge on each capacitor.
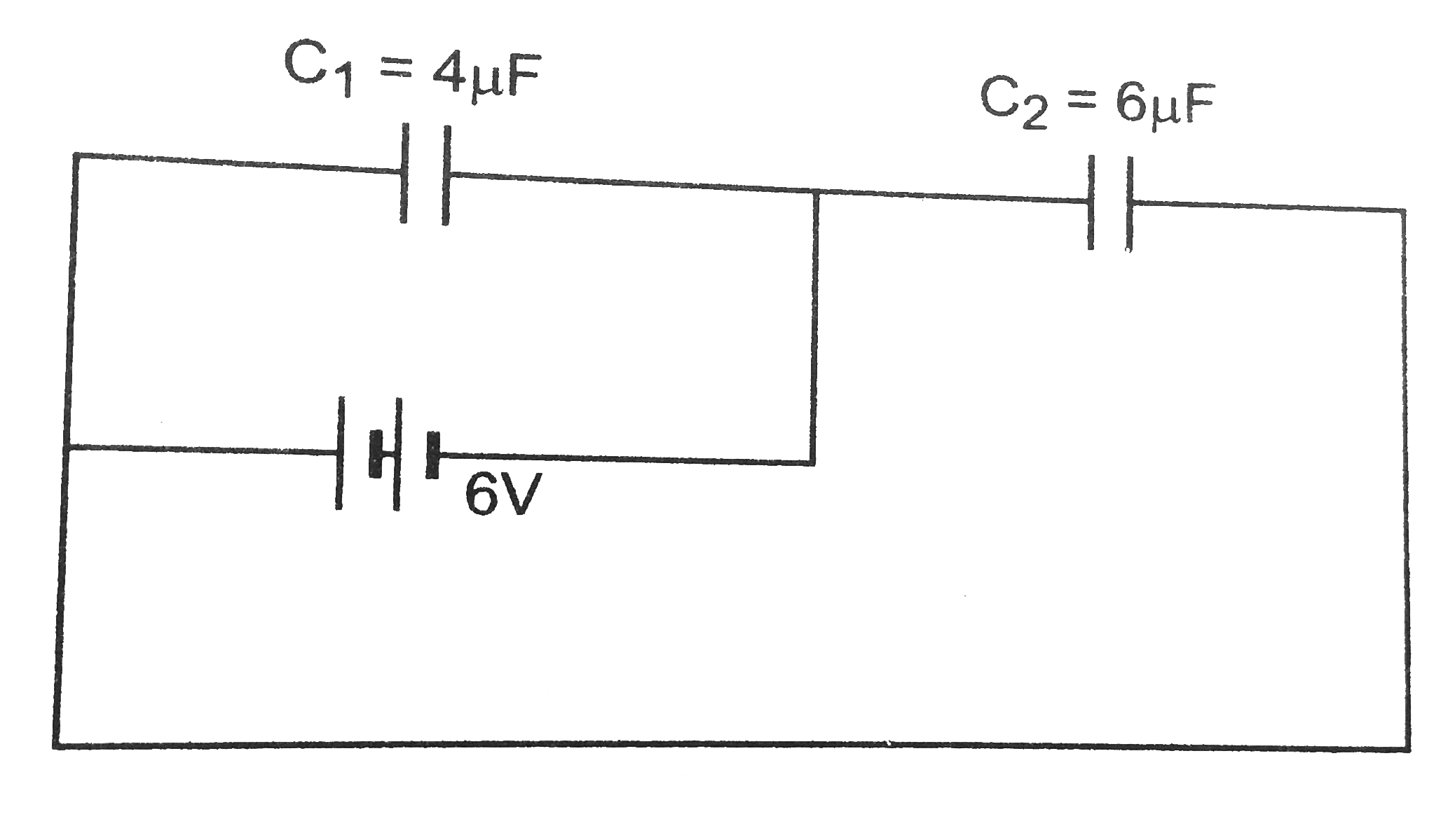
View Solution
