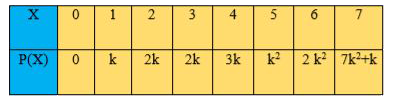
A random variable X has the following probability distribution:Determine (i) k (ii) P(X<3)(iii) P(X>6) (iv) P(0<X<3)
As we know, for any probablity distribution,
∑P(X)=1
So, for given distribution,
0+k+2k+2k+3k+k2+2k2+7k2+k=1
10k2+9k−1=0
10k2+10k−k−1=0
10k(k+1)−1(k+1)=0
(10k−1)(k+1)=0
As, k can not be negative, k=110
(ii) P(X<3)=P(X=0)+P(X=1)+P(X=2)
=3k=310
(iii) P(X>6)=P(X=7)
=7k2+k=7100+110=17100
(iv)P(0<X<3)=P(X=1)+P(X=2)
=3k=310
Topper's Solved these Questions
- PROBABILITYBOOK - NCERT ENGLISHCHAPTER - PROBABILITYEXERCISE - EXERCISE 13.2
18 Videos
- PROBABILITYBOOK - NCERT ENGLISHCHAPTER - PROBABILITYEXERCISE - EXERCISE 13.5
15 Videos
- MATRICESBOOK - NCERT ENGLISHCHAPTER - MATRICESEXERCISE - All Questions
105 Videos
- RELATIONS AND FUNCTIONSBOOK - NCERT ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - EXERCISE 1.3
14 Videos
Similar Questions
A random variable X has the following probability distribution:Determine (i) k (ii) P(X<3)(iii) P(X>6) (iv) P(0<X<3)
View SolutionA random variable X has the following probability distribution :

Determine
(i) k (ii) P(X<3)
(iii) P(X>6) (iv) P(0<X<3).
View SolutionA random variable X has the following probability distribution:
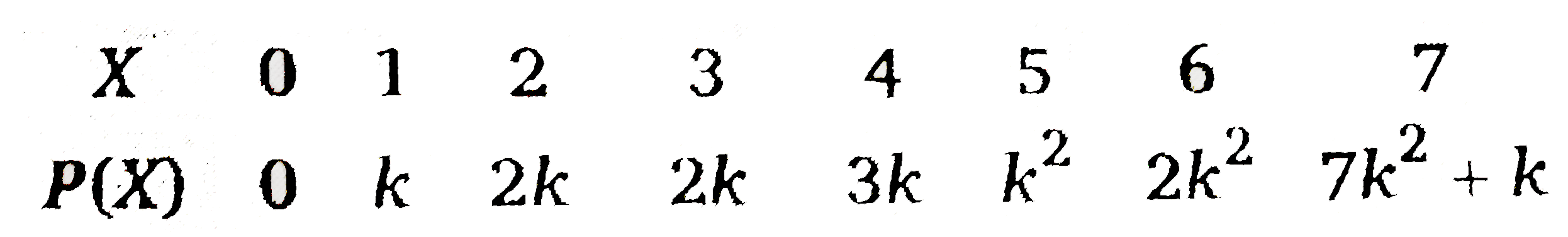
Determine :
(i) k
(ii) P(X<3)
(iii) P(X>6)
(iv) P(0<X<3)
View SolutionA random variable X has the following probability distribution:
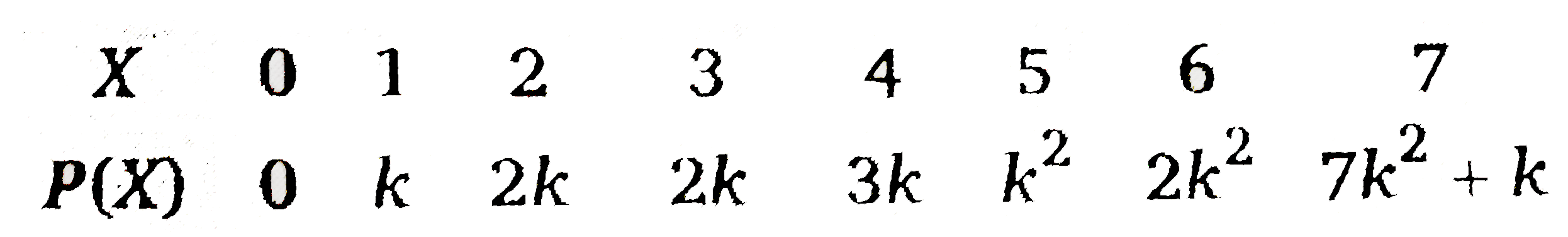
Determine :
(i) k
(ii) P(X<3)
(iii) P(X>6)
(iv) P(0<X<3)
View SolutionA random variable X has the following probability distribution:

Determine (i)k,(ii)P(X<3),(iii)P(0<X<3),(iv)P(X>4).
View SolutionA random variable X has the following probability distribution:
Determine : (i) k (ii) P(X<3) (iii) P(X>4)
View SolutionA random variable X has the following probability distribution find K.

View SolutionA random variable X has the following probability distribution :

determine the value of a
View SolutionA random variable X has the following probability distribution. Then the value of (i) k (ii) P(X<3) (iii) P(X>6) (iv) P(0<X<3)

View SolutionA random variable 'X' has the following probability distribution :

The values of k is
View Solution
