In Fig. 6.37, if QT⊥PR,∠TQR=40∘and∠SPR=30∘, find x and y.
To solve the problem step-by-step, we will use the properties of triangles and the relationships between angles.
Step 1: Identify the angles in triangle QTR
In triangle QTR:
- We know that QT is perpendicular to PR, which means angle QTR = 90°.
- We are given that angle TQR = 40°.
Step 2: Use the angle sum property of triangles
The sum of the angles in a triangle is always 180°. Therefore, we can write the equation for triangle QTR:
Angle QTR+Angle TQR+Angle TRQ=180°
Substituting the known values:
90°+40°+x=180°
Step 3: Solve for x
Now, we can simplify the equation:
130°+x=180°
Subtract 130° from both sides:
x=180°−130°=50°
Step 4: Find angle y using the exterior angle theorem
Next, we need to find angle y (angle PSQ). According to the exterior angle theorem, the exterior angle is equal to the sum of the two opposite interior angles. Here, angle PSQ is the exterior angle at point S.
The interior angles are:
- Angle SPR = 30°
- Angle SRP = x = 50°
So we can write:
y=Angle SPR+Angle SRP
Substituting the known values:
y=30°+50°=80°
Final Answers
Thus, we have:
- x=50°
- y=80°
In triangle QTR:
- We know that QT is perpendicular to PR, which means angle QTR = 90°.
- We are given that angle TQR = 40°.
The sum of the angles in a triangle is always 180°. Therefore, we can write the equation for triangle QTR:
Angle QTR+Angle TQR+Angle TRQ=180°
90°+40°+x=180°
Now, we can simplify the equation:
130°+x=180°
Subtract 130° from both sides:
x=180°−130°=50°
Next, we need to find angle y (angle PSQ). According to the exterior angle theorem, the exterior angle is equal to the sum of the two opposite interior angles. Here, angle PSQ is the exterior angle at point S.
- Angle SPR = 30°
- Angle SRP = x = 50°
y=Angle SPR+Angle SRP
Substituting the known values:
y=30°+50°=80°
Thus, we have:
- x=50°
- y=80°
Topper's Solved these Questions
- LINES AND ANGLESBOOK - NCERT ENGLISHCHAPTER - LINES AND ANGLESEXERCISE - Exercise 6.1
6 Videos
- LINES AND ANGLESBOOK - NCERT ENGLISHCHAPTER - LINES AND ANGLESEXERCISE - EXERCISE 6.2
6 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBOOK - NCERT ENGLISHCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - Exercise 4.1
2 Videos
- NCERT THEOREMSBOOK - NCERT ENGLISHCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 10.12
1 Videos
Similar Questions
In Figure, if QT⊥PR, ∠TQR=40∘ and ∠SPR=30∘, find x and y.
View SolutionIf Figure, if QT⊥PR,∠TQR=400 AND ∠SPR=300, find x and y. Figure
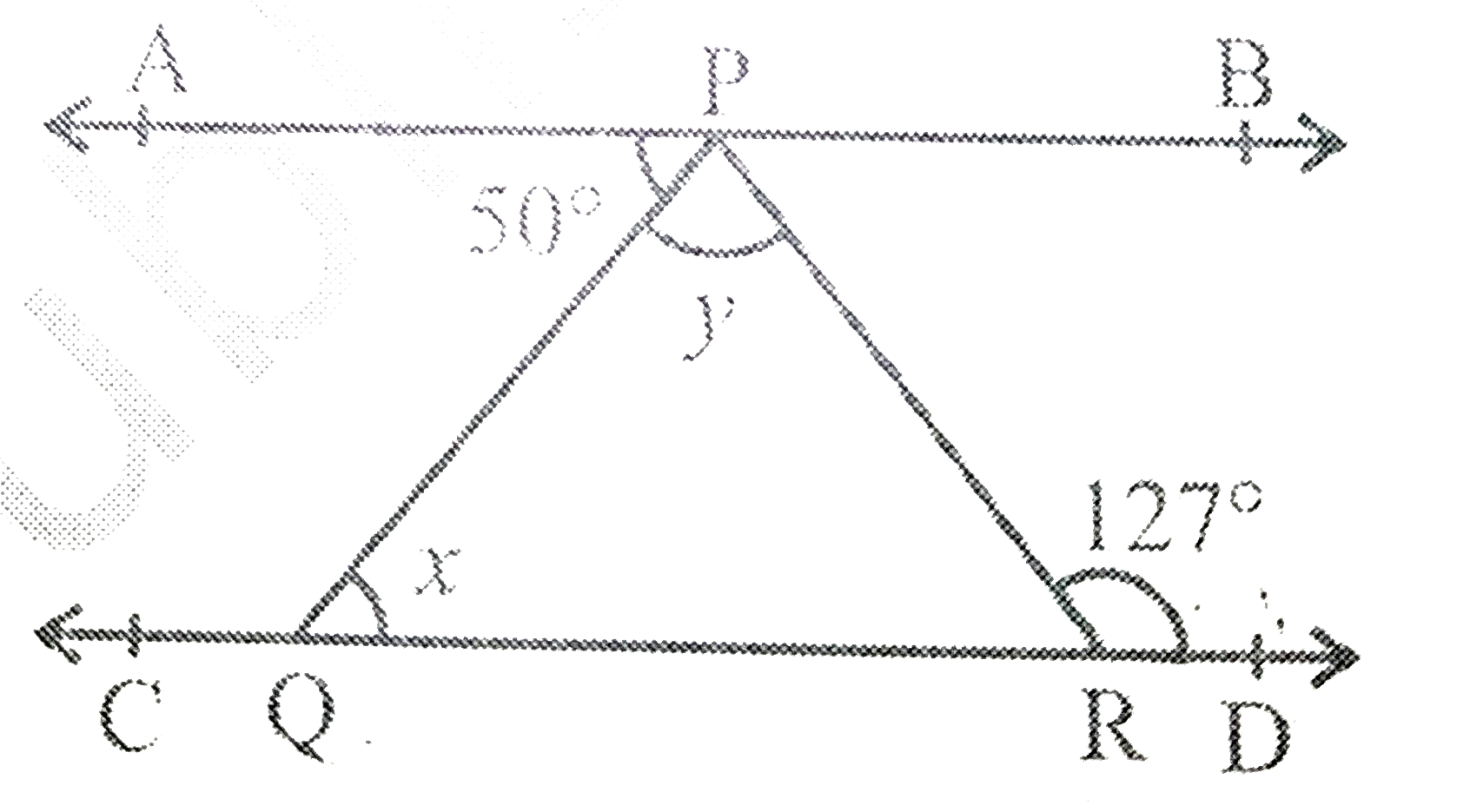
View SolutionIn Fig. 6.32, if AB∣∣CD,∠APQ=50∘and∠PRD=127∘, find x and y.
View SolutionIn Fig. 6.31, if PQ∣∣ST,∠PQR=110∘ and∠RST=130∘, find ∠QRS.

View SolutionIn Fig. 6.24, if PQ∣∣RS,∠MXQ=135∘ and∠MYR=40∘,find ∠XMY.
View SolutionIn Fig. 6.43, if PQ⊥PS,PQ∣∣SR,∠SQR=28∘ and ∠QRT=65∘, then find the values of x and y.

View SolutionIn Figure, if PQ∣∣RS, ∠MXQ=135∘and ∠MYR=40∘,find ∠XMY
View SolutionIn Figure, if PQ⊥PS, PQSR, ∠SQR=280and ∠QRT=650, then find the values of x and y
View SolutionIn figure, if PQ⊥PS,PQ∣∣SR,∠SQR=280 and ∠QRT=650, then find the values of x and y. Figure
View SolutionIn Fig. if ST∣∣QR . Find PS
View Solution
