ABCD is a cyclic quadrilateral (see Figure). Find the angles of the cyclic quadrilateral.
To find the angles of the cyclic quadrilateral ABCD, we will use the properties of cyclic quadrilaterals and the given expressions for the angles.
1. Identify the angles:
- Angle A = 4y+20
- Angle B = 3y−5
- Angle C = −4x
- Angle D = −7x+5
2. Use the property of cyclic quadrilaterals:
The sum of opposite angles in a cyclic quadrilateral is 180∘. Therefore, we can set up the following equations:
- Equation 1: Angle A+Angle C=180∘
- Equation 2: Angle B+Angle D=180∘
3. Set up the equations:
- From Equation 1:
(4y+20)+(−4x)=180
Simplifying this gives:
4y−4x+20=180⟹4y−4x=160⟹y−x=40(Equation 1)
- From Equation 2:
(3y−5)+(−7x+5)=180
Simplifying this gives:
3y−5−7x+5=180⟹3y−7x=180(Equation 2)
4. Solve the equations:
- From Equation 1, we can express y in terms of x:
y=x+40
- Substitute y in Equation 2:
3(x+40)−7x=180
Expanding this gives:
3x+120−7x=180⟹−4x+120=180
Rearranging gives:
−4x=60⟹x=−15
5. Find y:
- Substitute x back into Equation 1:
y=−15+40=25
6. Calculate the angles:
- Angle A:
A=4y+20=4(25)+20=100+20=120∘
- Angle B:
B=3y−5=3(25)−5=75−5=70∘
- Angle C:
C=−4x=−4(−15)=60∘
- Angle D:
D=−7x+5=−7(−15)+5=105+5=110∘
7. Verify the angles:
- Check if the opposite angles sum to 180∘:
- A+C=120+60=180∘
- B+D=70+110=180∘
Final Angles:
- Angle A = 120∘
- Angle B = 70∘
- Angle C = 60∘
- Angle D = 110∘
- Angle A = 4y+20
- Angle B = 3y−5
- Angle C = −4x
- Angle D = −7x+5
The sum of opposite angles in a cyclic quadrilateral is 180∘. Therefore, we can set up the following equations:
- Equation 1: Angle A+Angle C=180∘
- Equation 2: Angle B+Angle D=180∘
- From Equation 1:
(4y+20)+(−4x)=180
Simplifying this gives:
4y−4x+20=180⟹4y−4x=160⟹y−x=40(Equation 1)
(3y−5)+(−7x+5)=180
Simplifying this gives:
3y−5−7x+5=180⟹3y−7x=180(Equation 2)
- From Equation 1, we can express y in terms of x:
y=x+40
3(x+40)−7x=180
Expanding this gives:
3x+120−7x=180⟹−4x+120=180
Rearranging gives:
−4x=60⟹x=−15
- Substitute x back into Equation 1:
y=−15+40=25
- Angle A:
A=4y+20=4(25)+20=100+20=120∘
- Angle B:
B=3y−5=3(25)−5=75−5=70∘
- Angle C:
C=−4x=−4(−15)=60∘
- Angle D:
D=−7x+5=−7(−15)+5=105+5=110∘
- Check if the opposite angles sum to 180∘:
- A+C=120+60=180∘
- B+D=70+110=180∘
- Angle A = 120∘
- Angle B = 70∘
- Angle C = 60∘
- Angle D = 110∘
Topper's Solved these Questions
- PAIR OF LINEAR EQUATIONS IN TWO VARIABLESBOOK - NCERT ENGLISHCHAPTER - PAIR OF LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - EXERCISE 3.4
2 Videos
- NCERT THEOREMSBOOK - NCERT ENGLISHCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 10.1
2 Videos
- POLYNOMIALSBOOK - NCERT ENGLISHCHAPTER - POLYNOMIALSEXERCISE - EXERCISE 2.4
5 Videos
Similar Questions
The sum of either pair of opposite angles of a cyclic quadrilateral is 1800 OR The opposite angles of a cyclic quadrilateral are supplementary.
View SolutionIn Figure, ABCD is a cyclic quadrilateral. Find the value of a and b.
View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral whose side AB is the diameter of the circle . If ∠ADC=140∘ , then find the value of ∠BAC.

View SolutionThe quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic.
View SolutionIf ABCD is a cyclic quadrilateral then find the value of sinA+sinB−sinC−sinD
View SolutionIf ABCD is a cyclic quadrilateral, then find the value of sinA+sinB−sinC−sinD
View SolutionIf ABCD is a cyclic quadrilateral, then the value of cosA-cosB+cosC-cosD is equal to
View SolutionABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC=140∘, than ∠BAC is equal to
View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral and AB is the diameter of the circle. If ∠APC=120∘, then find the value of ∠CAB.
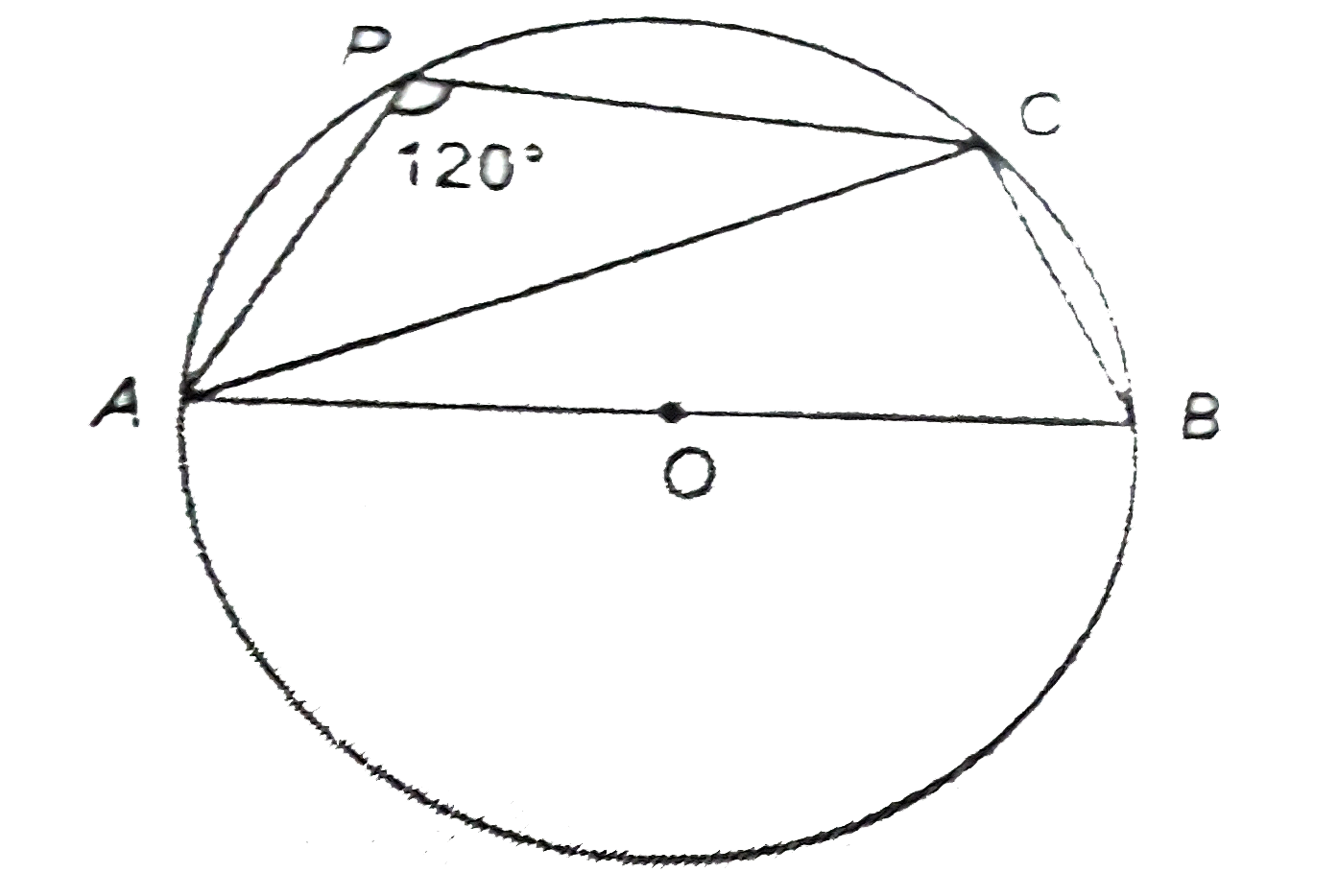
View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral. If ∠DBC=60∘ and ∠BAC=40∘ , then find the value of ∠BCD .
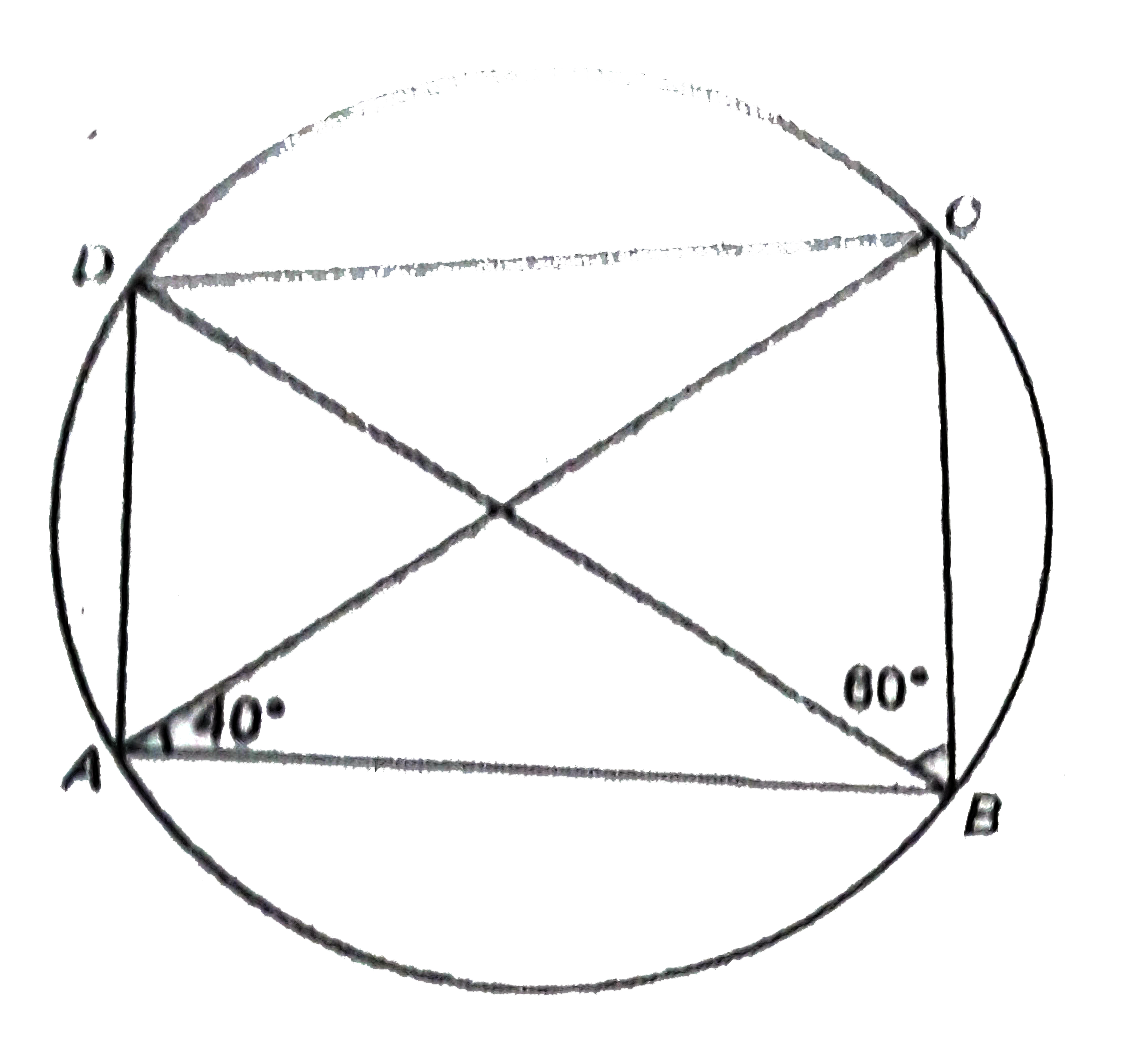
View Solution
