The following distribution shows the daily pocket allowance of children of a locality. The mean pocket allowance is Rs 18. Find the missing frequency f.
To find the missing frequency f in the given distribution of daily pocket allowances of children, we will follow these steps:
Step 1: Set Up the Frequency Distribution Table
We have the following intervals and their corresponding frequencies:
| Interval | Frequency (f) |
|------------|---------------|
| 11 - 13 | 7 |
| 13 - 15 | 6 |
| 15 - 17 | 9 |
| 17 - 19 | 13 |
| 19 - 21 | f |
| 21 - 23 | 5 |
| 23 - 25 | 4 |
Step 2: Calculate the Midpoint (xi) for Each Interval
The midpoint xi for each interval is calculated as follows:
- For 11 - 13: x1=11+132=12
- For 13 - 15: x2=13+152=14
- For 15 - 17: x3=15+172=16
- For 17 - 19: x4=17+192=18
- For 19 - 21: x5=19+212=20
- For 21 - 23: x6=21+232=22
- For 23 - 25: x7=23+252=24
Step 3: Calculate fi⋅xi for Each Interval
Now, we multiply the frequency by the midpoint for each interval:
| Interval | Frequency (f) | Midpoint (xi) | fi⋅xi |
|------------|---------------|-----------------------|----------------------|
| 11 - 13 | 7 | 12 | 7⋅12=84 |
| 13 - 15 | 6 | 14 | 6⋅14=84 |
| 15 - 17 | 9 | 16 | 9⋅16=144 |
| 17 - 19 | 13 | 18 | 13⋅18=234 |
| 19 - 21 | f | 20 | 20f |
| 21 - 23 | 5 | 22 | 5⋅22=110 |
| 23 - 25 | 4 | 24 | 4⋅24=96 |
Step 4: Calculate Total Frequency and Total fi⋅xi
Total frequency N=7+6+9+13+f+5+4=44+f
Total fi⋅xi=84+84+144+234+20f+110+96=752+20f
Step 5: Set Up the Mean Equation
The mean is given as 18. We can set up the equation:
Mean=Total fi⋅xiTotal Frequency=18
Substituting the values we calculated:
752+20f44+f=18
Step 6: Cross Multiply and Solve for f
Cross multiplying gives:
752+20f=18(44+f)
Expanding the right side:
752+20f=792+18f
Rearranging terms:
752−792=18f−20f
−40=−2f
Dividing both sides by -2:
f=20
Conclusion
The missing frequency f for the interval 19 - 21 is 20.
---
We have the following intervals and their corresponding frequencies:
|------------|---------------|
| 11 - 13 | 7 |
| 13 - 15 | 6 |
| 15 - 17 | 9 |
| 17 - 19 | 13 |
| 19 - 21 | f |
| 21 - 23 | 5 |
| 23 - 25 | 4 |
The midpoint xi for each interval is calculated as follows:
- For 13 - 15: x2=13+152=14
- For 15 - 17: x3=15+172=16
- For 17 - 19: x4=17+192=18
- For 19 - 21: x5=19+212=20
- For 21 - 23: x6=21+232=22
- For 23 - 25: x7=23+252=24
Now, we multiply the frequency by the midpoint for each interval:
|------------|---------------|-----------------------|----------------------|
| 11 - 13 | 7 | 12 | 7⋅12=84 |
| 13 - 15 | 6 | 14 | 6⋅14=84 |
| 15 - 17 | 9 | 16 | 9⋅16=144 |
| 17 - 19 | 13 | 18 | 13⋅18=234 |
| 19 - 21 | f | 20 | 20f |
| 21 - 23 | 5 | 22 | 5⋅22=110 |
| 23 - 25 | 4 | 24 | 4⋅24=96 |
Total frequency N=7+6+9+13+f+5+4=44+f
The mean is given as 18. We can set up the equation:
Cross multiplying gives:
The missing frequency f for the interval 19 - 21 is 20.
Similar Questions
The following distribution shows the daily pocket allowance given to the children of a multistorey building. The average pocket allowance is Rs 18.00. Find out the missing frequency: Class 11-13 13-15 15-17 17-19 19-21 21-23 23-25 interval: Frequency: 7 6 9 13 - 5 4
View SolutionIf the mean of the following distribution is 7.5, find the missing frequency f

View SolutionThe following table gives the distribution of 100 families according to expenditure. If mode of the distribution is 124, find the missing frequencies.

View SolutionConsider the following distribution of daily wages of 50 workers of a factory.Find the mean daily wages of the workers of the factor}- by using an appropriate method.
View SolutionThe mean of the following distribution is 18. Find the frequency f of the class 19−21.
View SolutionThe table below shows the daily expenditure on food of 30 households in a locality:
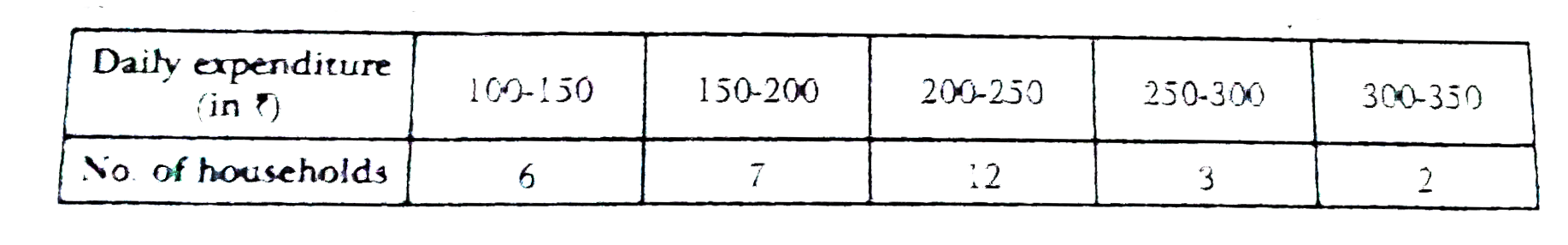
Find the mean daily expenditure on food.
View SolutionThe mean of the following distribution is 62.8 and the sum of all the frequencies is 50. Find the missing frequencies f1 and f2

View SolutionThe mean of the following distribution is 50 but the frequency f1andf2 in classes 20-40 and 60-80, resepectively are not known. Find these frequencies, if the sum of all the fequencies is 120
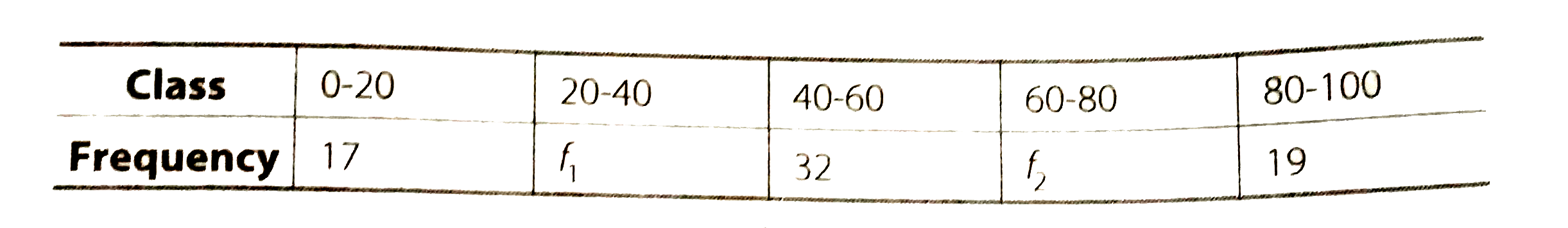
View SolutionThe table below shows the daily expenditure on food of 25 households in a locality.Find the mean daily expenditure on food by a suitable method.
View SolutionThe mean of the following frequency distribution is 50, but the frequencies f1andf2 in class 20-40 and 60-80 respectively are not known. Find these frequencies.

Given that the sum of frequencies is 120.
View Solution
