Fig. 12.26 depicts a racing track whose left and right ends are semicircular. The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find :(i) the distance around the track along its inner edge(ii) the area of the track.
To solve the problem step by step, we will find the distance around the track along its inner edge and then calculate the area of the track.
Step 1: Understanding the Track Configuration
The racing track consists of two straight segments and two semicircular ends. The distance between the two inner parallel line segments is 60 m, and each segment is 106 m long.
Step 2: Calculate the Radius of the Semicircles
The distance between the two inner parallel segments is the diameter of the semicircles. Therefore, the radius R of the semicircles is:
R=602=30 m
Step 3: Calculate the Circumference of the Semicircles
The circumference of a full circle is given by 2πR. For a semicircle, it is half of that:
Circumference of one semicircle=πR=π×30=30π m
Since there are two semicircles, the total length contributed by the semicircles is:
Total length of semicircles=2×30π=60π m
Step 4: Calculate the Total Distance Around the Track
The total distance around the track along its inner edge is the sum of the lengths of the two straight segments and the two semicircles:
Total distance=Length of straight segments+Total length of semicircles
Total distance=106+106+60π=212+60π m
Step 5: Substitute the Value of π
Using π≈227:
60π≈60×227=13207 m
Now, substituting this back into the total distance:
Total distance=212+13207=1484+13207=28047≈400.57 m
Step 6: Calculate the Area of the Track
The area of the track can be calculated by finding the area of the outer rectangle and subtracting the area of the inner rectangle, then adding the area of the two semicircles.
1. Dimensions of the Outer Rectangle:
- Length = 106 m
- Width = 60 m (distance between the inner segments) + 10 m (width of the track) + 10 m (width of the track) = 80 m
- Area of the outer rectangle = 106×80=8480 m2
2. Dimensions of the Inner Rectangle:
- Length = 106 m
- Width = 60 m
- Area of the inner rectangle = 106×60=6360 m2
3. Area of the Two Semicircles:
- Larger semicircle radius = 40 m (since the total width is 80 m)
- Smaller semicircle radius = 30 m
- Area of larger semicircles = 2×12π(402)=2×12π×1600=1600π
- Area of smaller semicircles = 2×12π(302)=2×12π×900=900π
4. Total Area of the Track:
Area of track=Area of outer rectangle−Area of inner rectangle+Area of larger semicircles−Area of smaller semicircles
=8480−6360+1600π−900π
=8480−6360+700π
=2120+700π
5. Substituting π:
=2120+700×227=2120+2200=4320 m2
Final Answers:
(i) The distance around the track along its inner edge is approximately 400.57 m.
(ii) The area of the track is 4320 m².
The racing track consists of two straight segments and two semicircular ends. The distance between the two inner parallel line segments is 60 m, and each segment is 106 m long.
The distance between the two inner parallel segments is the diameter of the semicircles. Therefore, the radius R of the semicircles is:
R=602=30 m
The circumference of a full circle is given by 2πR. For a semicircle, it is half of that:
Circumference of one semicircle=πR=π×30=30π m
Since there are two semicircles, the total length contributed by the semicircles is:
Total length of semicircles=2×30π=60π m
The total distance around the track along its inner edge is the sum of the lengths of the two straight segments and the two semicircles:
Total distance=Length of straight segments+Total length of semicircles
Total distance=106+106+60π=212+60π m
Using π≈227:
60π≈60×227=13207 m
Now, substituting this back into the total distance:
Total distance=212+13207=1484+13207=28047≈400.57 m
The area of the track can be calculated by finding the area of the outer rectangle and subtracting the area of the inner rectangle, then adding the area of the two semicircles.
- Length = 106 m
- Width = 60 m (distance between the inner segments) + 10 m (width of the track) + 10 m (width of the track) = 80 m
- Area of the outer rectangle = 106×80=8480 m2
- Length = 106 m
- Width = 60 m
- Area of the inner rectangle = 106×60=6360 m2
- Larger semicircle radius = 40 m (since the total width is 80 m)
- Smaller semicircle radius = 30 m
- Area of larger semicircles = 2×12π(402)=2×12π×1600=1600π
- Area of smaller semicircles = 2×12π(302)=2×12π×900=900π
Area of track=Area of outer rectangle−Area of inner rectangle+Area of larger semicircles−Area of smaller semicircles
=8480−6360+1600π−900π
=8480−6360+700π
=2120+700π
=2120+700×227=2120+2200=4320 m2
(i) The distance around the track along its inner edge is approximately 400.57 m.
(ii) The area of the track is 4320 m².
Topper's Solved these Questions
- AREAS RELATED TO CIRCLESBOOK - NCERT ENGLISHCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - Exercise 12.2
14 Videos
- AREAS RELATED TO CIRCLESBOOK - NCERT ENGLISHCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - EXERCISE 12.1
5 Videos
- ARITHMETIC PROGRESSIONSBOOK - NCERT ENGLISHCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - All Questions
65 Videos
Similar Questions
The inside perimeter of a running track (shown in figure) is 400m. The length of each of the straight portion is 90m and the ends are semi-circles. If track is everywhere 14m wide, find the area of the track. Also, find the length of the outer running track.
View SolutionThe inner circumference of a circular track is 440 m. The track is 3.5m wide all around Find the outer circumference and also the area of the track.
View SolutionThe inner perimeter of a running track (shown in figure) is 400 m. The length of each of the straight portion is 90 m and the ends are semicircular. If the track is everywhere 14 m wide, find the area of the track. Also, find the length of the outer running track.

View SolutionThe inside perimeter of a running track (shown in figure) is 400m. The length of each of the straight portion is 90m and the ends are semi-circles. If track is everywhere 14m wide, find the area of the track. Also, find the length of the outer running track.
View SolutionAn athletic track 14 m wide consists of two straight sections 120 m long joining and semicircular ends inner diameter 35 m . find area of track
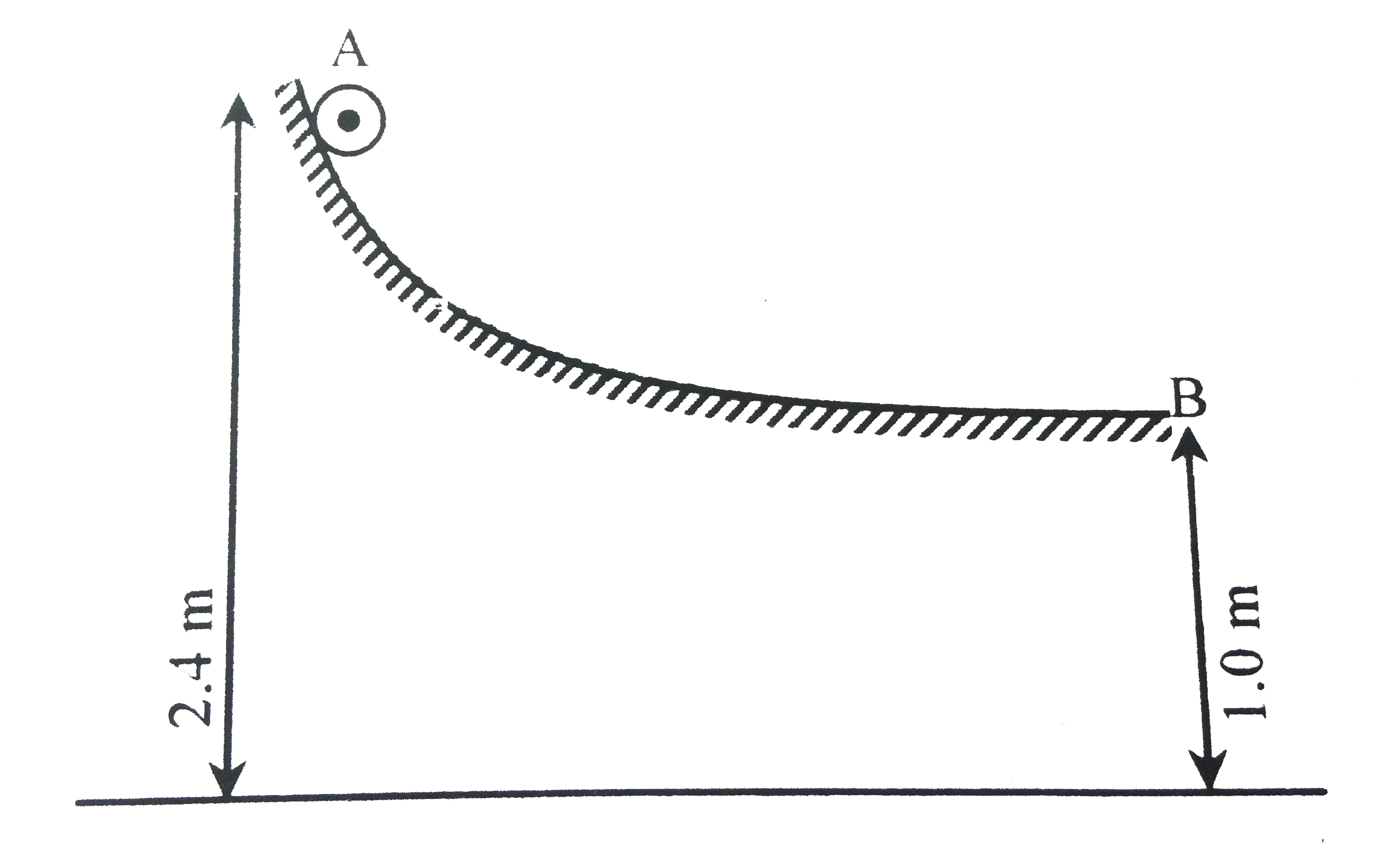
View SolutionA small sphere rolls down without slipping from the top of a track in a vertical plane. The track has an elevated section and a horizontal part. The horizontall part is 1.0 meter above the ground level and the top of the track is 2.4 meter above the ground. Find the distance on the ground with respect to a point B( which is vetically below the end A of the track as shown in fig.) where the sphere lands.
 .
.
(A) 1m
(B) 2m
( C) 3m
(D) 4m.
View SolutionTwo parallel rails of a railway track insulated from each other and with the ground are connected to a millivoltmeter. The distance between the rails is one metre. A train is traveling with a velocity of 72kmph along the track. The reading of the millivoltmetre (in mV) is : (Vertical component of the earth's magnetic induction is 2×10−5T)
View SolutionThe area of a trapezium is 384 cm2 . Its parallel sides are in the ratio 3:5 and the perpendicular distance between them is 12cm. Find the length of each one of the parallel sides.
View SolutionA race track is in the form of a ring whose inner circumference is 352 m and the outer circumference is 396 m. Find the width of the track.
View SolutionA race track is in the form of a ring whose inner circumference is 352 m, and the outer circumference is 396 m. Find the width of the track.
View Solution