Show that the bisectors of angles of a parallelogram form a rectangle.
To show that the bisectors of the angles of a parallelogram form a rectangle, we will follow these steps:
Step 1: Define the Parallelogram
Let ABCD be a parallelogram where A, B, C, and D are the vertices. The angles at these vertices are denoted as ∠A, ∠B, ∠C, and ∠D.
Step 2: Identify the Angle Bisectors
Let the angle bisectors of ∠A, ∠B, ∠C, and ∠D meet at points P, Q, R, and S respectively. Thus, we have:
- P is on the bisector of ∠A
- Q is on the bisector of ∠B
- R is on the bisector of ∠C
- S is on the bisector of ∠D
Step 3: Use the Properties of Angles in a Parallelogram
In a parallelogram, opposite angles are equal, and adjacent angles are supplementary. Therefore, we have:
- ∠A+∠D=180∘
- ∠B+∠C=180∘
- ∠A=∠C
- ∠B=∠D
Step 4: Calculate Angles at Points P, Q, R, and S
Using the property of angle bisectors, we can express the angles at points P, Q, R, and S:
- ∠SAP=12∠A
- ∠BAP=12∠A
- Therefore, ∠SAP+∠BAP=∠A
- Similarly, for Q, R, and S:
- ∠SBQ=12∠B
- ∠QBR=12∠B
- ∠RCP=12∠C
- ∠DSR=12∠D
Step 5: Show that Each Angle is 90∘
We need to show that:
- ∠PSQ=90∘
- ∠QRP=90∘
- ∠RSP=90∘
- ∠PQR=90∘
Using the angle relationships:
1. From ∠A+∠D=180∘:
- ∠SAP+∠SAD+∠DAP=180∘
- Thus, 12∠A+12∠D=90∘
- Therefore, ∠PSQ=90∘
2. Similarly, for ∠B and ∠C:
- ∠QRP=90∘
- ∠RSP=90∘
- ∠PQR=90∘
Step 6: Conclusion
Since all angles at points P, Q, R, and S are 90∘, the quadrilateral PQRS is a rectangle.
Let ABCD be a parallelogram where A, B, C, and D are the vertices. The angles at these vertices are denoted as ∠A, ∠B, ∠C, and ∠D.
Let the angle bisectors of ∠A, ∠B, ∠C, and ∠D meet at points P, Q, R, and S respectively. Thus, we have:
- P is on the bisector of ∠A
- Q is on the bisector of ∠B
- R is on the bisector of ∠C
- S is on the bisector of ∠D
In a parallelogram, opposite angles are equal, and adjacent angles are supplementary. Therefore, we have:
- ∠A+∠D=180∘
- ∠B+∠C=180∘
- ∠A=∠C
- ∠B=∠D
Using the property of angle bisectors, we can express the angles at points P, Q, R, and S:
- ∠SAP=12∠A
- ∠BAP=12∠A
- Therefore, ∠SAP+∠BAP=∠A
- Similarly, for Q, R, and S:
- ∠SBQ=12∠B
- ∠QBR=12∠B
- ∠RCP=12∠C
- ∠DSR=12∠D
We need to show that:
- ∠PSQ=90∘
- ∠QRP=90∘
- ∠RSP=90∘
- ∠PQR=90∘
1. From ∠A+∠D=180∘:
- ∠SAP+∠SAD+∠DAP=180∘
- Thus, 12∠A+12∠D=90∘
- Therefore, ∠PSQ=90∘
- ∠QRP=90∘
- ∠RSP=90∘
- ∠PQR=90∘
Since all angles at points P, Q, R, and S are 90∘, the quadrilateral PQRS is a rectangle.
Similar Questions
Prove that the quadrilateral formed by the bisectors of the angles of a parallelogram is a rectangle.

View SolutionProve that the quadrilateral formed by the bisectors of the angles of a parallelogram is a rectangle.

View SolutionThe angle bisectors of a parallelogram form a rectangle.
View Solution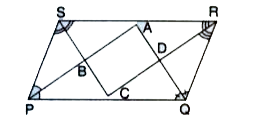
In the alongside diagram, the bisectors of interior angles of the parallelogram PQRS enclose a quadrilateral ABCD.
Show that:
(i) ∠PSB+∠SPB=90∘
(ii) ∠PBS=90∘
(iii) ∠ABC=90∘
(iv) ∠ADC=90∘
(v) ∠A=90∘
(vi) ABCD is a rectangle
thus, the bisectors of the angles of a parallelogram enclose a rectangle.
View SolutionProve that the bisectors of opposite angles of a parallelogram are parallel.
View SolutionAB and CD are two parallel lines and a transversal 'l' intersects these lines at X and Y respectively Prove that the bisectors of interior angles from a parallelogram whose each angle is 90∘.
View SolutionThe opposite angles of a parallelogram are equal.
View SolutionShow that, in a parallelogram ABCD, the internal and external bisectors of ∠Aand∠B from a rectangle.
View SolutionProve that the bisectors of the interior angles of a rectangle form a square.
View SolutionAB,CD are two parallel lines and a transversal l intersects AB at X and CD at Y Prove that the bisectors of the interior angles form a parallelogram, with all its angles right angles i.e., it is a rectangle.
View Solution
