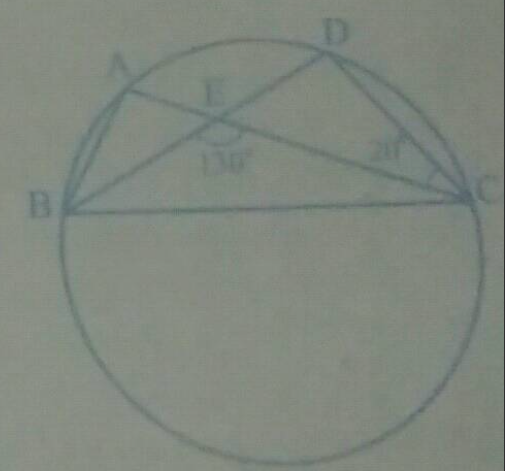
A, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠BEC =130∘ and ∠ECD=20∘ Find ∠BAC∘
Please refer to video for the figure.
Here, ∠BEC=130∘and∠ECD=20∘
∠AEB+∠BEC=180∘(Sum of angles formed by a straight line is 180^@)
∠AEB=180−130=50∘
Also, ∠ABD=∠ACD as these angles are subtended by a same chord on the circle.
So,∠ABD=∠ABE=20∘
Now, in ΔAEB
∠ABE+∠AEB+∠EAB=180∘
EAB+50+20=180
EAB=110∘
So, ∠BAC=EAB=110∘
Similar Questions
In Fig. 10.39, A, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠BEC\ =\ 130o and ∠ECD\ =\ 20⊙ Find ∠BAC.
View SolutionIn a ABC,D and E are points on sides ABandAC respectively such that BD=CE. If ∠B=∠C, show that DE∣∣BC.
View SolutionIn ABC, D and E are points on sides AB and AC respectively such that AD×EC=AE×DB . Prove that DEBC .
View SolutionThe points A,B,C,D,E are marked on the circumference of a circle in clockwishdirection such that ?ABC=130∘and∠CDE=110∘. The measure of ∠ACE degress is
View SolutionD and E are points on sides AB and AC respectively of ΔABC such that ar (DBC) = ar (EBC). Prove that DE∣∣BC.
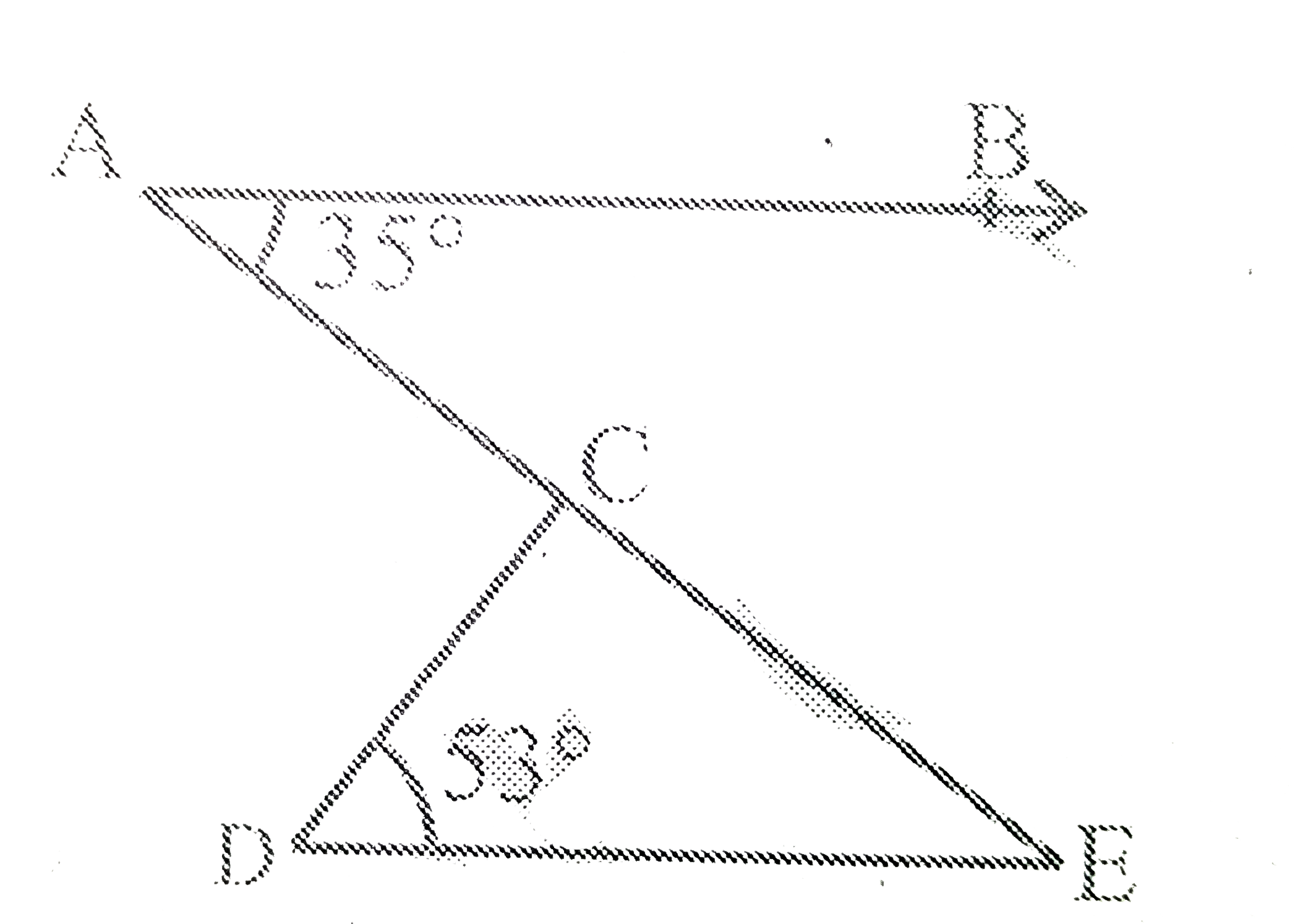
View SolutionIn Fig. 6.41, if AB∣∣DE,∠BAC=35∘ and ∠CDE=53∘, find ∠DCE.
View SolutionIn a ABC , D and E are points on the sides AB and AC respectively such that DE∣∣BC If AD=6 cm , DB=9 cm and AE=8 cm , find AC .
View SolutionIn a ABC , D and E are points on the sides AB and AC respectively such that DE/BC If AD=4 , AE=8 , DB=x−4 , and EC=3x−19 , find x .
View SolutionD and E are points on sides AB and AC respectively of ΔABCsuch thatar (DBC) = ar (EBC). Prove that DE ∣∣ BC.
View SolutionIf D and E are points on sides AB and AC respectively of a triangle ABC such that DE∣∣BC and BD=CE . Prove that ABC is isosceles.
View Solution
