Question

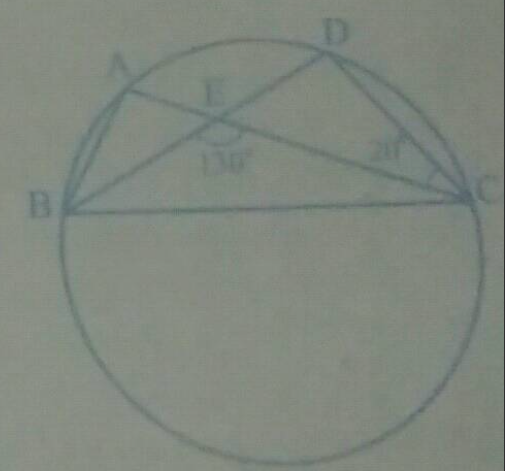
In Fig. 10.39,
A, B, C and D are four points on a circle. AC and BD intersect at a point E
such that $\angle BEC\text{}=\text{}130o$
and $\angle ECD\text{}=\text{}20\odot$
Find $\angle BAC\stackrel{.}{}$

Explanation

To solve the problem, we need to find the angle $$\angle BAC$$ given the angles $$\angle BEC={130}^{\circ }$$ and $$\angle ECD={20}^{\circ }$$.

1. Identify the Angles:
We have \( \angle BEC = 130^\circ \) and \( \angle ECD = 20^\circ \).

2. Use the Exterior Angle Theorem:
In triangle \( EDC \), the exterior angle \( \angle BEC \) is equal to the sum of the two opposite interior angles \( \angle ECD \) and \( \angle CDE \):
\( \angle BEC = \angle ECD + \angle CDE \)
Substituting the known values:
\( 130^\circ = 20^\circ + \angle CDE \)

3. Solve for \( \angle CDE \):
Rearranging the equation gives:
\( \angle CDE = 130^\circ - 20^\circ = 110^\circ \)

4. Relate \( \angle CDE \) to \( \angle BDC \):
Since \( \angle CDE \) is the same as \( \angle BDC \) (they are vertically opposite angles), we have:
\( \angle BDC = 110^\circ \)

5. Use the Inscribed Angle Theorem:
The angle \( \angle BAC \) is equal to \( \angle BDC \) because they subtend the same arc \( BC \) in the circle. Therefore:
\( \angle BAC = \angle BDC = 110^\circ \)

Conclusion:
Thus, the measure of \( \angle BAC \) is \( 110^\circ \).