The points A,B,C,D,E are marked on the circumference of a circle in clockwishdirection such that ?ABC=130∘and∠CDE=110∘. The measure of ∠ACE degress is
50∘
60∘
70∘
80∘
The correct Answer is:A, B
To find the measure of angle ∠ACE given the angles ∠ABC=130∘ and ∠CDE=110∘, we can follow these steps:
Step 1: Identify the Given Angles
We have:
- ∠ABC=130∘
- ∠CDE=110∘
Step 2: Analyze the Quadrilateral ABCE
Since points A,B,C,E are on the circumference of the circle, we can form quadrilateral ABCE. In any cyclic quadrilateral, the sum of the opposite angles is 180∘.
Step 3: Find ∠AEC
Using the property of cyclic quadrilaterals:
∠ABC+∠AEC=180∘
Substituting the known value:
130∘+∠AEC=180∘
Solving for ∠AEC:
∠AEC=180∘−130∘=50∘
Step 4: Analyze the Quadrilateral CDEA
Now, consider quadrilateral CDEA. Again, using the property of cyclic quadrilaterals:
∠CDE+∠CAE=180∘
Substituting the known value:
110∘+∠CAE=180∘
Solving for ∠CAE:
∠CAE=180∘−110∘=70∘
Step 5: Find ∠ACE
Now we can use the angles in triangle ACE:
∠CAE+∠AEC+∠ACE=180∘
Substituting the known values:
70∘+50∘+∠ACE=180∘
Combining the angles:
120∘+∠ACE=180∘
Solving for ∠ACE:
∠ACE=180∘−120∘=60∘
Final Answer
The measure of ∠ACE is 60∘.
---
We have:
- ∠ABC=130∘
- ∠CDE=110∘
Since points A,B,C,E are on the circumference of the circle, we can form quadrilateral ABCE. In any cyclic quadrilateral, the sum of the opposite angles is 180∘.
Using the property of cyclic quadrilaterals:
∠ABC+∠AEC=180∘
Substituting the known value:
130∘+∠AEC=180∘
Solving for ∠AEC:
∠AEC=180∘−130∘=50∘
Now, consider quadrilateral CDEA. Again, using the property of cyclic quadrilaterals:
∠CDE+∠CAE=180∘
Substituting the known value:
110∘+∠CAE=180∘
Solving for ∠CAE:
∠CAE=180∘−110∘=70∘
Now we can use the angles in triangle ACE:
∠CAE+∠AEC+∠ACE=180∘
Substituting the known values:
70∘+50∘+∠ACE=180∘
Combining the angles:
120∘+∠ACE=180∘
Solving for ∠ACE:
∠ACE=180∘−120∘=60∘
The measure of ∠ACE is 60∘.
Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - RACE 3
10 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - RACE 4
10 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Race 21
14 Videos
- LOGARITHMSBOOK - ALLENCHAPTER - LOGARITHMSEXERCISE - All Questions
92 Videos
- SEQUENCE AND PROGRESSIONBOOK - ALLENCHAPTER - SEQUENCE AND PROGRESSIONEXERCISE - Exercise (JA)
12 Videos
Similar Questions
Knowledge Check
If A, B, C, D, E and F are 6 distinct points on the circumference of a circle, how many different chords can be drawn using any 2 of the 6 points ?
A6B12C15D30
If A is the area and C is the circumference of a circle, then its radius is
(a)AC
(b) 2AC
(c)3AC
(d) 4AC
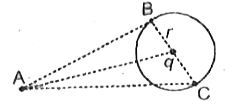
View SolutionA point charge q is held at the centre of a circle of radius r. B,C are two points on the circumference of the circle and A is a point outsdie the circle . If WAB charge qe from A to B and WAC represents the workdone from A to C ,then
View SolutionIn Fig. 10.39, A, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠BEC\ =\ 130o and ∠ECD\ =\ 20⊙ Find ∠BAC.
View SolutionFind the diameter of a circle whose circumference is (a)12.56 cm (b) 88 m (c)11.0 km
View SolutionIn Figure, O is the centre of the circle such that ∠AOC =1300, then ∠ABC= (a)1300 (b) 1150 (c) 650 (d) 1650
View SolutionAB is a diameter of a circle and C is any point on the circumference of the circle. Then a) the area of ABC is maximum when it is isosceles b) the area of ABC is minimum when it is isosceles c) the perimeter of ABC is minimum when it is isosceles d) none of these
View SolutionA, B, C, D are four consecutive points on a circle such that AB=CD. Prove that AC=BD
View Solution