The record of a weather station shows that out of the past 250 onsecutivedays, its weather forecasts were correct 175 times.(i) What is the probability that on a given day it was correct?(ii) What is the probability that it was not correct on a given day?
To solve the problem step by step, we will calculate the probabilities as follows:
Step 1: Calculate the Probability that the Forecast was Correct
1. Identify the number of days the forecast was correct: According to the data, the weather forecasts were correct 175 times.
2. Identify the total number of days: The total number of days recorded is 250.
3. Use the probability formula: The probability (P) that the forecast was correct is given by the formula:
P(Correct)=Number of correct forecastsTotal number of days
4. Substitute the values:
P(Correct)=175250
5. Simplify the fraction:
P(Correct)=710=0.7
Step 2: Calculate the Probability that the Forecast was Not Correct
1. Identify the number of days the forecast was not correct: To find this, subtract the number of correct forecasts from the total number of days:
Number of incorrect forecasts=Total days−Number of correct forecasts=250−175=75
2. Use the probability formula: The probability that the forecast was not correct is given by:
P(Not Correct)=Number of incorrect forecastsTotal number of days
3. Substitute the values:
P(Not Correct)=75250
4. Simplify the fraction:
P(Not Correct)=310=0.3
Final Answers
- (i) The probability that on a given day the forecast was correct is 0.7.
- (ii) The probability that it was not correct on a given day is 0.3.
1. Identify the number of days the forecast was correct: According to the data, the weather forecasts were correct 175 times.
2. Identify the total number of days: The total number of days recorded is 250.
3. Use the probability formula: The probability (P) that the forecast was correct is given by the formula:
P(Correct)=Number of correct forecastsTotal number of days
4. Substitute the values:
P(Correct)=175250
5. Simplify the fraction:
P(Correct)=710=0.7
1. Identify the number of days the forecast was not correct: To find this, subtract the number of correct forecasts from the total number of days:
Number of incorrect forecasts=Total days−Number of correct forecasts=250−175=75
2. Use the probability formula: The probability that the forecast was not correct is given by:
P(Not Correct)=Number of incorrect forecastsTotal number of days
3. Substitute the values:
P(Not Correct)=75250
4. Simplify the fraction:
P(Not Correct)=310=0.3
- (i) The probability that on a given day the forecast was correct is 0.7.
- (ii) The probability that it was not correct on a given day is 0.3.
Topper's Solved these Questions
Similar Questions
The record of a weather station shows that out of the past 250 consecutive days, its weather forecast were correct 175 times. What is the probability that on a given day (i) it was correct? (ii) it was not correct?
View SolutionThe record of a weather station shows that out of the past 250 consecutive days, its weather forecast were correct 175 times. What is the probability that on a given day (i) it was correct? (ii) it was not correct?
View SolutionThere is 30% chance that it rains on any particular day. What is the probability what where is at least one rainy day within a period of 7 days ? Given that there is at least one rainy day, What is the probability that there are at least two rainy days ?
View SolutionA child has die whose six faces show the letters as given below:
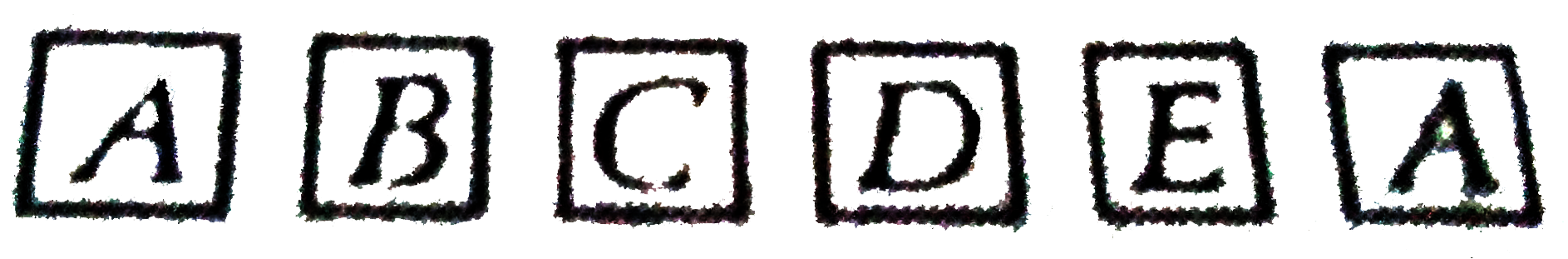
The die is thrown once. What is the probability of getting (i) A, (ii) D?
View SolutionIn answering a question on a multiple choice test, a student either knows the answer or guesses. Let 35 be the probability that he knows the answer and 25 be the probability that he guesses. Assuming that a student who guesses at the answer will be correct with probability 13 , what is the probability that the student knows the answer given that he answered it correctly
View SolutionIn answering a question on a multiple choice test a student either knows the answer or guesses. Let the probability that he knows the answer is 34 and probability that he guesses is 14. Assuming that a student who guesses the answer and given correct answer is 14. What is the probability that student knows the answer given that he answered it correctly?
View Solution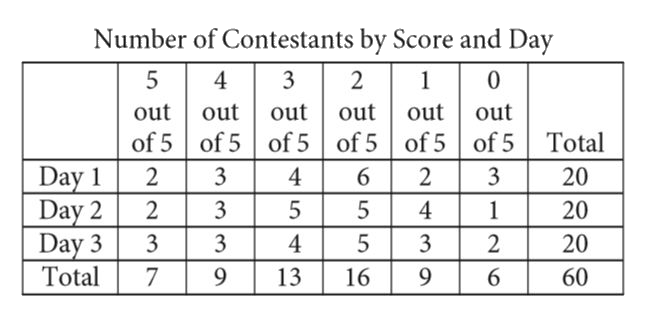
The same 20 contestants, on each of 3 days, answered 5 questions in order to win a prize. Each contestant received 1 point for each correct answer. The number of contestants receiving a given score on each day is shown in the table above.
No contestant received the same score on two different days. If a contestant is selected at random, what is the probability that the selected contestant received a score of 5 on Day 2 or Day 3, given that the contestant received a score of 5 on one of the three days?
View SolutionOn a multiple choice examination with three possible answers (out of which only one is correct) for each of the five questions, what is the probability that a candidate would get four or more correct answers just guessing?
View SolutionTwo customers are visiting a particular shop in the same week (Monday to Saturday). Each is equally likely to visit the shop on any one day as on another. What is the probability that both will visit the shop on: (i) the same day? (ii) different days?
View SolutionBulbs are packed in cartons each containing 40 bulbs, seven hundred cartons were examined for defective bulbs and the results are given in the following table.

One carton was selected at random. What is the probability that it has
i) no defective bulb?
ii) defective bulbs from 2-6?
iii) defective bulbs less than 4?
View Solution
