An insurance company selected 2000 drivers at random (i.e., without any preference of one driver over another) in a particular city to find a relationship between age and accidents. The data obtained are given in the following table:A g e\ o
To solve the problem, we need to calculate the probabilities for three different cases based on the data provided about drivers and their accident records. Let's break down each case step by step.
Step 1: Understand the Data
We have a total of 2000 drivers categorized by age groups and the number of accidents they had in one year.
Step 2: Calculate Probability for Case 1
Case 1: The probability of a driver being aged 18 to 29 years and having exactly three accidents in one year.
1. Identify the number of favorable outcomes:
- From the data, the number of drivers aged 18 to 29 with exactly three accidents is 70.
2. Identify the total number of outcomes:
- The total number of drivers is 2000.
3. Calculate the probability:
P(18 to 29 years and 3 accidents)=Number of favorable outcomesTotal outcomes=702000=0.035
Step 3: Calculate Probability for Case 2
Case 2: The probability of a driver being aged 30 to 50 years and having one or more accidents in a year.
1. Identify the number of favorable outcomes:
- From the data, we need to sum the number of drivers aged 29 to 50 with:
- 1 accident: 118
- 2 accidents: 65
- 3 accidents: 20
- More than 3 accidents: 21
- Total favorable outcomes = 118 + 65 + 20 + 21 = 224.
2. Identify the total number of outcomes:
- The total number of drivers is still 2000.
3. Calculate the probability:
P(30 to 50 years and 1 or more accidents)=2242000=0.112
Step 4: Calculate Probability for Case 3
Case 3: The probability of a driver having no accidents in one year.
1. Identify the number of favorable outcomes:
- From the data, we need to sum the number of drivers with zero accidents:
- Age 18 to 28: 395
- Age 29 to 50: 520
- Age above 50: 390
- Total favorable outcomes = 395 + 520 + 390 = 1305.
2. Identify the total number of outcomes:
- The total number of drivers is still 2000.
3. Calculate the probability:
P(No accidents)=13052000=0.6525
Summary of Probabilities
- Case 1 Probability: P(18 to 29 years and 3 accidents)=0.035
- Case 2 Probability: P(30 to 50 years and 1 or more accidents)=0.112
- Case 3 Probability: P(No accidents)=0.6525
We have a total of 2000 drivers categorized by age groups and the number of accidents they had in one year.
Case 1: The probability of a driver being aged 18 to 29 years and having exactly three accidents in one year.
- From the data, the number of drivers aged 18 to 29 with exactly three accidents is 70.
- The total number of drivers is 2000.
P(18 to 29 years and 3 accidents)=Number of favorable outcomesTotal outcomes=702000=0.035
Case 2: The probability of a driver being aged 30 to 50 years and having one or more accidents in a year.
- From the data, we need to sum the number of drivers aged 29 to 50 with:
- 1 accident: 118
- 2 accidents: 65
- 3 accidents: 20
- More than 3 accidents: 21
- Total favorable outcomes = 118 + 65 + 20 + 21 = 224.
- The total number of drivers is still 2000.
P(30 to 50 years and 1 or more accidents)=2242000=0.112
Case 3: The probability of a driver having no accidents in one year.
- From the data, we need to sum the number of drivers with zero accidents:
- Age 18 to 28: 395
- Age 29 to 50: 520
- Age above 50: 390
- Total favorable outcomes = 395 + 520 + 390 = 1305.
- The total number of drivers is still 2000.
P(No accidents)=13052000=0.6525
- Case 1 Probability: P(18 to 29 years and 3 accidents)=0.035
- Case 2 Probability: P(30 to 50 years and 1 or more accidents)=0.112
- Case 3 Probability: P(No accidents)=0.6525
Similar Questions
An insurance company selected 2000 drivers at random (i.e., without any preference of one driver over another) in a particular city to find a relationship between age and accidents. The data obtained are given in the following table: Find the probabilities of the following events for a driver chosen at random from the city: (i) The driver being in the age group 18−29 years and having exactly 3 accidents in one year. (ii) The driver being in the age group of 30−50 year and having one or more accidents in a year. (iii) The number of drivers having no accidents in one year
View SolutionAn insurance company selected 2000 drivers at random in a particular city to find a relationship between age and accidents. The obtained are given in the following table: Age of Drivers (in years) Accidents in one year 0 1 2 3 over 3 18-29 30-50 above 50 440 505 360 160 125 45 110 60 35 61 22 15 35 18 9 Find the probability of the following events for a driver chosen at random from the life city: i) being 18-29 years of age and having exactly 3 accidents in one year. ii) being 30-50 years of age and having one or more accidents in a year. iii) having no accidents in one year.
View SolutionA company selected 4000 households at random and surveyed them to find out a relationship between income level and the number of televisions sets in a home. The information, so obtained is listed in the following table.

Find the probability
i) of a household earning Rs 10000- Rs 14999 per year and having exactly one television.
ii) of a household earning Rs 25000 and more per year owning 2 televisions.
iii) of a household not having any television.
View SolutionA company selected 2400 families at random and survey them to determine a relationship between income level and the number of vehicles in a home. The information gathered is listed in the table below: If a family is chosen, find the probability that the family is: (i) earning Rs.10000-13000 per month and owning exactly 2 vehicles. (ii) earning Rs. 16000 or more per month and owning exactly 1 vehicle (iii) Earning less than Rs. 7000 per month and does not own any vehicle. (iv) earning Rs.13000-16000 per month and owning more than 2 vehicle. (v) owning not more than 1 vehicle. (vi) owning at least one vehicle.
View SolutionA company selected 2400 families at random and survey them to determine a relationship between income level and the number of vehicles in a home. The information gathered is listed in the table below: Monthly income (in Rs.) Vehicles per family 0 1 2 Above 2 Less than 7000 10 160 25 0 7000-10000 0 305 27 2 10000-13000 1 535 29 1 13000-16000 2 469 29 25 16000 or more 1 579 82 88 If a family is chosen, find the probability that the family is: earning Rs. 10000-13000 per month and owning exactly 2 vehicles. earning Rs. 16000 or more per month and owning exactly 1 vehicles. Earning less than Rs. 7000 per month and does not own any vehicle. Earning Rs. 13000-16000 per month and owning more than 2 vehicle. owning not more than 1 vehicle owning at least one vehicle.
View SolutionA TV reporter was given a task to prepare a report on the rainfall of the city Dispur of India in a particular year. After collecting the data, he analyzed the data and prepared a report on the rainfall of the city. Using this report, he drew the following graph for a particular time period of 66 days
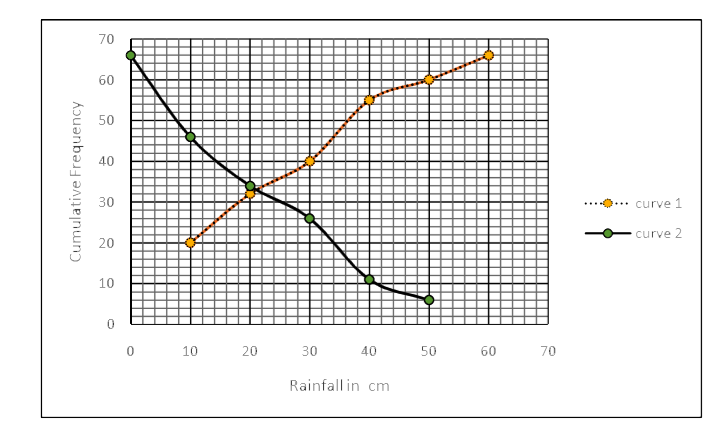
Based on the above graph, answer the following questions
(i) Identify less than type ogive and more than type ogive from the given graph.
(ii) Find the median rainfall of Dispur
(iii) Obtain the Mode of the data if mean rainfall is 23.4cm
View SolutionIn a metal in the solid state, such as a copper wire, the atoms are strongly bound to one another and occupý fixed positions. Some electrons (called the conductor electrons) are free to move in the body of the metal while the other are strongly bound to their atoms. In good conductors, the number of free electrons is very large of the order of 1028 electrons per cubic metre in copper. The free electrons are in random motion and keep colliding with atoms. At room temperature, they move with velocities of the order of 105 m/s. These velocities are completely random and there is not net flow of charge in any directions. If a potential difference is maintained between the ends of the metal wire (by connecting it across a battery), an electric field is set up which accelerates the free electrons: These accelerated electrons frequently collide with the atoms of the conductor, as a result, they acquire a constant speed called the drift speed which is given by Ve= 1/enA where I = current in the conductor due to drifting electrons, e = charge of electron, n = number of free electrons per unit volume of the conductor and A = area of cross-section of the conductor. A constant potential difference is maintained between the ends of a conductor having nonuniform cross-section. Which of the following quantities will not change along the length of the conductor
View SolutionWhen an atom or an ion is missing from its nomal lattice site a lattice vacanecy (Schottky defect) is created. In stoichmeteric ionic crystals, a vacancy of one ion has to be accompanied by the vacancy of the oppositely charge ion in order to maintain electrical neutrality.
In a Frenkel defect an ion leaves its position in the lattice and occupies an interstitial void. This id the Frenkel defect commonly found along with the Schottky defects and interstitial. In pure alkali halides. Frenked defects are not found since the ions cannot get into the interstitial sites. Frenkel defects are found in silver halides because of the small size of the Ag+ ion. Unike Schottky defects, Frenkel defect do not change the density of the solids. in certain ionic solids (e.g., AgBr) both schottky and Frenkel defect occur.
The Defects idiscussed above do not disturb the stoichiometery of the crystalline material. there is large variety of non-stoichiometric inorganic solids which contains an excess or deficienty of one of the elements. Such solids showing deviations from the ideal stoichiometric composition from an important group of solids. For example in the vanadium oxide, VOx,x can be anywehere between 0.6 and 1.3 there are solids such as difficult to prepare in the soichiometric omposition thus, the ideal composition in compounds such as FeO is difficult to obtain (normally we get a compositiion of Fe(0.95)O but it may range from Fe0.93O to Fe0.96O). Non-stoichiometric behavious is most commonly found for transition metal compounds through is also known for some lathanoids and actinoids.
Zinc oxide loses oxygen reversible at high temperature and turns yellow in colour. the excess metal is accomodated interstitial, giving rise to electrons trapped in the neighbourhood, the enchanced electrical conductivity of the non-stoichiometric ZnO arises from these electrons.
Anion vacancies in alkali halides are produced by heating the alkali halid crystals in an atmosphere of the alkali metal vapour. when the metal atoms deposit on the surface they diffuse into the cystal and after ionisation the alkali metal ion occupies cationic vacancy whereas electron occupies anionic vacancy. Electrons trapped i anion vacancies are referred to as F-centers (From Farbe the German word for colouf) that gives rise to interesting colour in alkali halides. Thus, the excess of potassium i KCl makes the crystal appear violet and the excess of lithium in LiCl makes it pink.
Which of the following is most appropritate crystal to show Frenkel defect ?
View SolutionRead the following paragraph and answer the questions given below ,
Stable equilibrium is of various types . Mechanical equilibrium is achieved when all particles are at rest and total potential energy of the system is minimum . At any stage where particles are at rest but the system is not at stable equilibrium as it can reduce its potential energy by reverting to another position, is called metastable equilibrium . Thermal equilibrium is result from the absence of temperature gradients in the system. Chemical equilibrium is obtained when no further reaction occurs between reacting substances, i.e forward and reverse rates of reaction are equal.
When steam with solid iron at high temperature Fe3O4(s) and hydrogen gas are produced . But the reaction never goes to completion. This is because as the products are formed the reaction proceeds in reverse direction and when rate of reverse reaction is equal to rate of forward reaction , the concentration of reactants and products become constant and equilibrium is reached.
The primary objective of the passage is
View SolutionA right angled prism of refractive index μ1 is placed in a rectangular block of refractive index μ2 , which is surrounded by a medium of refractive index μ3 ,as shown in the figure . A ray of light 'e' enters the rectangular block at normal incidence . depending upon the relationship between μ1,μ2andμ3 , it takes one of the four possible paths 'ef' , 'eg' , 'eh' or 'ef'
_E01_228_Q01.png)
Match the paths in List I with conditions of refractive indices in List II and select the correct answer using the codes given below the lists:
{:("List" I , "List" II) , ( P. e rarr f , 1. mu_(1)gt sqrt(2mu_(2))) , ( Q. e rarr g , 2. mu_(2) gt mu_(1) "and" mu_(2) gt mu_(3)), ( R. e rarr f , 3. mu_(1) = mu_(2)), ( S. e rarr f , 4. mu_(2) lt mu_(1) lt sqrt(2mu_(2)) "and" mu_(2) gt mu_(3)):}<br>Codes:<br>{:( P , Q , R , S) , ((A) 2 , 3 , 1 , 4), ((B) 1 , 2 , 4 , 3) , ((C) 4 , 1 , 2 , 3) , ((D) 2, 3 , 4 , 1):}
View Solution
