Question

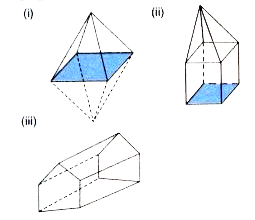
Verify Euler’s formula for these solids.

Answer

Eulers formula

Face + Vertices - Edges = `2`

`(1)`Face=`7`

Vertices=`10`

Edges=`15`

Eulers = `F+V-E=7+10-15=2`

`(2)` Face=`9`

Vertices=`9`

Edges=`16`

Eulers = `F+V-E=9+9-16=2.`

Explanation

To verify Euler's formula for the given solids, we will follow these steps:

Step 1: Understand Euler's Formula
Euler's formula states that for any convex polyhedron, the relationship between the number of faces (F), vertices (V), and edges (E) is given by:
\( F + V - E = 2 \)

Step 2: Identify the Values for the First Solid
For the first solid, we need to identify the number of faces, vertices, and edges:
- Faces (F) = 7
- Vertices (V) = 10
- Edges (E) = 15

Step 3: Substitute Values into Euler's Formula for the First Solid
Now, we substitute these values into Euler's formula:
\( F + V - E = 7 + 10 - 15 \)

Step 4: Calculate the Result for the First Solid
Now we perform the calculation:
\( 7 + 10 = 17 \)
\( 17 - 15 = 2 \)

Step 5: Verify the Result for the First Solid
Since we have:
\( F + V - E = 2 \)
This confirms that Euler's formula holds true for the first solid.

Step 6: Identify the Values for the Second Solid
Now, we repeat the process for the second solid:
- Faces (F) = 9
- Vertices (V) = 9
- Edges (E) = 16

Step 7: Substitute Values into Euler's Formula for the Second Solid
Substituting these values into Euler's formula:
\( F + V - E = 9 + 9 - 16 \)

Step 8: Calculate the Result for the Second Solid
Now we perform the calculation:
\( 9 + 9 = 18 \)
\( 18 - 16 = 2 \)

Step 9: Verify the Result for the Second Solid
Since we have:
\( F + V - E = 2 \)
This confirms that Euler's formula also holds true for the second solid.

Conclusion
Euler's formula is verified for both solids as follows:
- For the first solid: \( 7 + 10 - 15 = 2 \)
- For the second solid: \( 9 + 9 - 16 = 2 \)