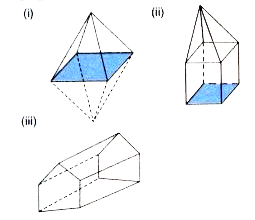
Verify Euler’s formula for each of the following polyhedrons: Figure (ii) Figure (iii) Figure
To verify Euler’s formula for the given polyhedrons, we will follow these steps for each figure:
Step 1: Understand Euler's Formula
Euler's formula states that for any convex polyhedron:
V+F=E+2
where:
- V = number of vertices
- F = number of faces
- E = number of edges
Step 2: Analyze the First Polyhedron
1. Count the vertices (V):
- There are 10 vertices.
2. Count the faces (F):
- There are 7 faces.
3. Count the edges (E):
- There are 15 edges.
4. Substitute the values into Euler's formula:
V+F=10+7=17
E+2=15+2=17
5. Since V+F=E+2 holds true, Euler's formula is verified for the first polyhedron.
Step 3: Analyze the Second Polyhedron
1. Count the vertices (V):
- There are 9 vertices.
2. Count the faces (F):
- There are 9 faces.
3. Count the edges (E):
- There are 16 edges.
4. Substitute the values into Euler's formula:
V+F=9+9=18
E+2=16+2=18
5. Since V+F=E+2 holds true, Euler's formula is verified for the second polyhedron.
Step 4: Analyze the Third Polyhedron
1. Count the vertices (V):
- There are 14 vertices.
2. Count the faces (F):
- There are 8 faces.
3. Count the edges (E):
- There are 20 edges.
4. Substitute the values into Euler's formula:
V+F=14+8=22
E+2=20+2=22
5. Since V+F=E+2 holds true, Euler's formula is verified for the third polyhedron.
Final Verification
- First Polyhedron: V+F=E+2 is verified as 17=17.
- Second Polyhedron: V+F=E+2 is verified as 18=18.
- Third Polyhedron: V+F=E+2 is verified as 22=22.
Euler's formula states that for any convex polyhedron:
V+F=E+2
where:
- V = number of vertices
- F = number of faces
- E = number of edges
1. Count the vertices (V):
- There are 10 vertices.
2. Count the faces (F):
- There are 7 faces.
3. Count the edges (E):
- There are 15 edges.
4. Substitute the values into Euler's formula:
V+F=10+7=17
E+2=15+2=17
5. Since V+F=E+2 holds true, Euler's formula is verified for the first polyhedron.
1. Count the vertices (V):
- There are 9 vertices.
2. Count the faces (F):
- There are 9 faces.
3. Count the edges (E):
- There are 16 edges.
4. Substitute the values into Euler's formula:
V+F=9+9=18
E+2=16+2=18
5. Since V+F=E+2 holds true, Euler's formula is verified for the second polyhedron.
1. Count the vertices (V):
- There are 14 vertices.
2. Count the faces (F):
- There are 8 faces.
3. Count the edges (E):
- There are 20 edges.
4. Substitute the values into Euler's formula:
V+F=14+8=22
E+2=20+2=22
5. Since V+F=E+2 holds true, Euler's formula is verified for the third polyhedron.
- First Polyhedron: V+F=E+2 is verified as 17=17.
- Second Polyhedron: V+F=E+2 is verified as 18=18.
- Third Polyhedron: V+F=E+2 is verified as 22=22.
Topper's Solved these Questions
Similar Questions
Knowledge Check
What is the Euler’s formula for a Polyhedron?
AF−V−E=0BF+V−E=2CF+V+E=1DF+V+E=3
Verify Euler's formula for the following three dimensional figures :
View SolutionFind the perimeter of each of the following shapes: Figure
View SolutionFind the area of each of the following figures.

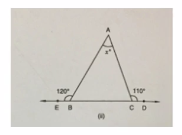
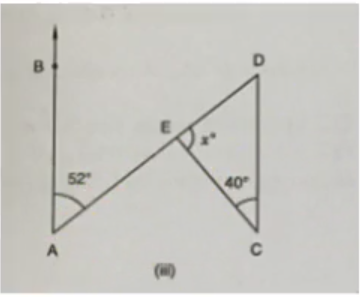
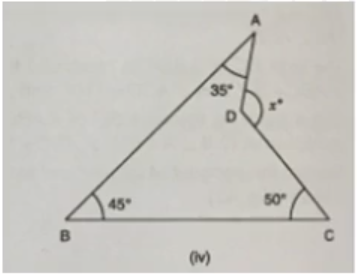
View SolutionCompute the value of x in each of the following figures:
View SolutionCompute the value of x in each of the following figures.

View SolutionFind the perimeter of each of the following figures.
View SolutionFind the measure of x in each of the following Figures
View Solution

