PQR is a triangle right angled at P. If PQ=10cmandPR=24cm, find QR
To find the length of side QR in triangle PQR, which is right-angled at P, we can use the Pythagorean theorem. The theorem states that in a right triangle, the square of the length of the hypotenuse (QR) is equal to the sum of the squares of the lengths of the other two sides (PQ and PR).
1. Identify the sides of the triangle:
- PQ = 10 cm (one leg)
- PR = 24 cm (the other leg)
- QR = ? (the hypotenuse)
2. Write the Pythagorean theorem:
QR2=PQ2+PR2
3. Substitute the known values into the equation:
QR2=(10)2+(24)2
4. Calculate the squares:
- 102=100
- 242=576
5. Add the squares together:
QR2=100+576=676
6. Take the square root to find QR:
QR=√676
7. Calculate the square root:
- The prime factorization of 676 is 22×132.
- Thus, √676=2×13=26.
8. Final answer:
QR=26 cm
- PQ = 10 cm (one leg)
- PR = 24 cm (the other leg)
- QR = ? (the hypotenuse)
QR2=PQ2+PR2
QR2=(10)2+(24)2
- 102=100
- 242=576
QR2=100+576=676
QR=√676
- The prime factorization of 676 is 22×132.
- Thus, √676=2×13=26.
QR=26 cm
Topper's Solved these Questions
- THE TRIANGLE AND ITS PROPERTIESBOOK - NCERT ENGLISHCHAPTER - THE TRIANGLE AND ITS PROPERTIESEXERCISE - EXERCISE 6.1
1 Videos
- THE TRIANGLE AND ITS PROPERTIESBOOK - NCERT ENGLISHCHAPTER - THE TRIANGLE AND ITS PROPERTIESEXERCISE - EXERCISE 6.2
2 Videos
- THE TRIANGLE AND ITS PROPERTIESBOOK - NCERT ENGLISHCHAPTER - THE TRIANGLE AND ITS PROPERTIESEXERCISE - EXERCISE 6.4
6 Videos
- SYMMETRYBOOK - NCERT ENGLISHCHAPTER - SYMMETRYEXERCISE - EXERCISE 14.2
2 Videos
Similar Questions
Knowledge Check
A steady current I goes through a wire loop PQR having shape of a right angle triangle with PQ=3x,PR=4xandQR=5x. If the magnitude of the magnetic field at P due to this loop is k(μ0I48πx), find the value of K.
A1B5C10D7
PQR is a triangle right-angled at P and M is a point on QR such that PM⊥QR. Show thatPM2=QM.MR.
View Solution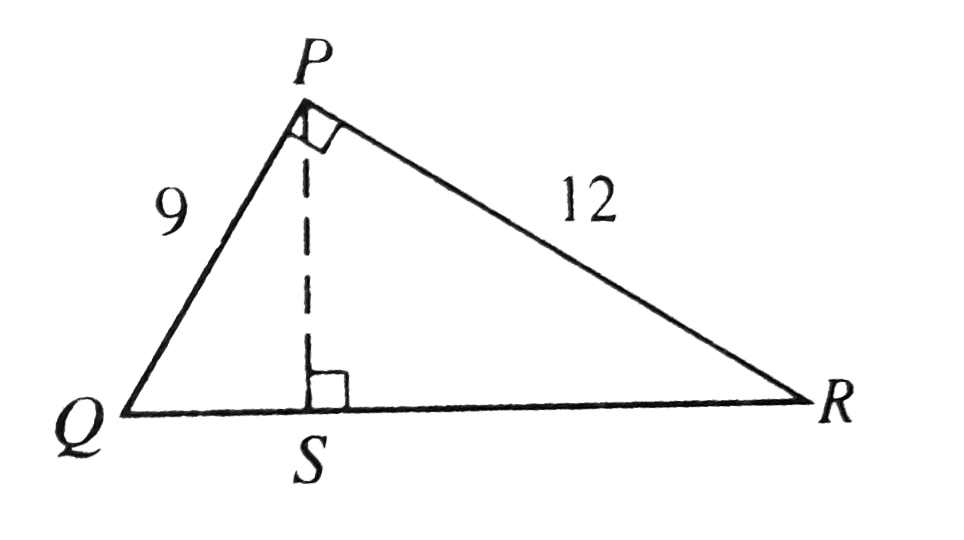
In the above figure, △PQR is a right triangle with the right angle at P . Line segment PS is an altitude , PQ=9 , and PR=12 . What is the area of △PQS ?
View SolutionIn the figure, given below, PQR is a right angled triangle right angled at Q. XY is parallel to QR, PQ = 6 cm, PY = 4 cm and PX : XQ = 1:2. Calculate the lengths of PR and QR.

View SolutionLet PQR be a right - angled isosceles triangle , right angled at P(2,1). If the equation of the line QR is 2x+y=3, then the equation representing the pair of lines PQ and PR is
View SolutionΔPQR is right angled isosceles triangle, right angled at R. Find value of sin P.
View SolutionIn the given figure PQRS is a cyclic quadrilateral PQ and SR produced meet at T. If SP=12cm and QR=4cm,
(iii) Find area of quadrilateral PQRS if area of ΔPTS=27cm2.

View SolutionGiven below are the lengths of the sides of three triangles. In each case, determine wheather the triangle is right angled or not.
(i) In ΔPQR,PQ=12cm,QR=13cm,PR=5cm.
(ii) In ΔDEF,DE=17cm,EF=15cm,DF=9cm.
(iii) In ΔABC,AB=37cm,BC=12cm,AC=35cm.
View Solution

