After rotating by 60° about a centre, a figure looks exactly the same as its original position. At what other angles will this happen for the figure?
To solve the problem step by step, we need to determine the other angles at which a figure will look the same after being rotated by 60 degrees around a center.
1. Understanding the Rotation:
We start with a figure that looks the same after being rotated by 60 degrees. This means that the figure has rotational symmetry.
Hint: Think about what rotational symmetry means for a shape.
2. Finding the Number of Rotational Symmetries:
The total angle of rotation in a circle is 360 degrees. To find the number of times the figure can be rotated to look the same, we divide 360 degrees by the angle of rotation (60 degrees).
Number of Rotational Symmetries=360∘60∘=6
Hint: Remember that the total angle in a circle is 360 degrees.
3. Calculating Other Angles:
Since the figure has 6 positions where it looks the same, we can find these positions by adding 60 degrees repeatedly to the initial angle of 0 degrees:
- First angle: 0∘
- Second angle: 0∘+60∘=60∘
- Third angle: 60∘+60∘=120∘
- Fourth angle: 120∘+60∘=180∘
- Fifth angle: 180∘+60∘=240∘
- Sixth angle: 240∘+60∘=300∘
- Finally, 300∘+60∘=360∘ (which brings us back to the starting position).
Hint: Keep adding 60 degrees until you reach 360 degrees.
4. Listing All Angles:
The angles at which the figure looks the same after rotation are:
- 0∘
- 60∘
- 120∘
- 180∘
- 240∘
- 300∘
Hint: Make sure to include the starting position (0 degrees) in your list.
Final Answer:
The other angles at which the figure looks the same after rotation are:
- 60∘
- 120∘
- 180∘
- 240∘
- 300∘
We start with a figure that looks the same after being rotated by 60 degrees. This means that the figure has rotational symmetry.
The total angle of rotation in a circle is 360 degrees. To find the number of times the figure can be rotated to look the same, we divide 360 degrees by the angle of rotation (60 degrees).
Number of Rotational Symmetries=360∘60∘=6
Since the figure has 6 positions where it looks the same, we can find these positions by adding 60 degrees repeatedly to the initial angle of 0 degrees:
- First angle: 0∘
- Second angle: 0∘+60∘=60∘
- Third angle: 60∘+60∘=120∘
- Fourth angle: 120∘+60∘=180∘
- Fifth angle: 180∘+60∘=240∘
- Sixth angle: 240∘+60∘=300∘
- Finally, 300∘+60∘=360∘ (which brings us back to the starting position).
The angles at which the figure looks the same after rotation are:
- 0∘
- 60∘
- 120∘
- 180∘
- 240∘
- 300∘
The other angles at which the figure looks the same after rotation are:
- 60∘
- 120∘
- 180∘
- 240∘
- 300∘
Topper's Solved these Questions
- SYMMETRYBOOK - NCERT ENGLISHCHAPTER - SYMMETRYEXERCISE - EXERCISE 14.1
9 Videos
- SYMMETRYBOOK - NCERT ENGLISHCHAPTER - SYMMETRYEXERCISE - EXERCISE 14.2
2 Videos
- SIMPLE EQUATIONSBOOK - NCERT ENGLISHCHAPTER - SIMPLE EQUATIONSEXERCISE - EXERCISE 4.4
3 Videos
- THE TRIANGLE AND ITS PROPERTIESBOOK - NCERT ENGLISHCHAPTER - THE TRIANGLE AND ITS PROPERTIESEXERCISE - EXERCISE 6.2
2 Videos
Similar Questions
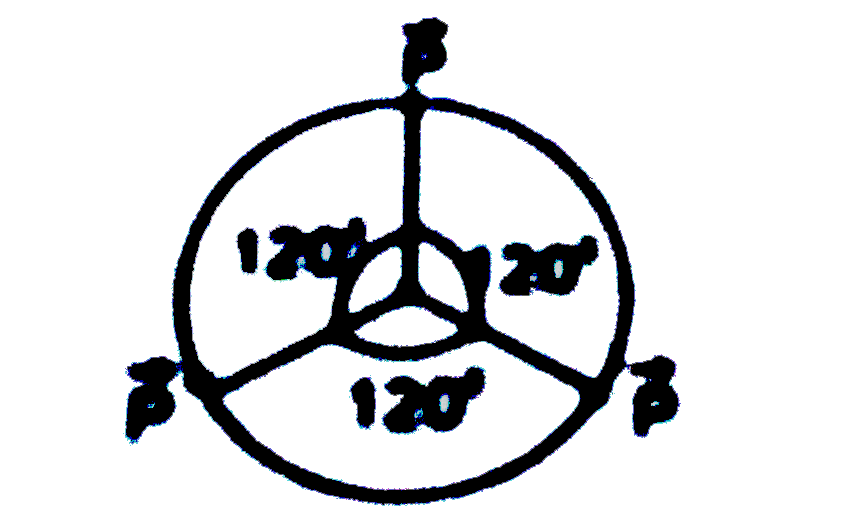
Three dipoles each of dipole moment of magnitude p are placed tangentially on a circle of radius R in its plae positioned at equal angle from each other as shown in the figure. Then the magnitude of electric field intensity at the centre of the circle will be :
View SolutionA vector of length l is turned through the angle θ about its tail. What is the change in the position vector of its head ?
View SolutionFigure shows the circular motion of a particle. The radius of the circle, the period, same of revolution and the initial position are indicated on the figure. The simple harmonic motion of the x-projection of the radius vector the rotating particle P is
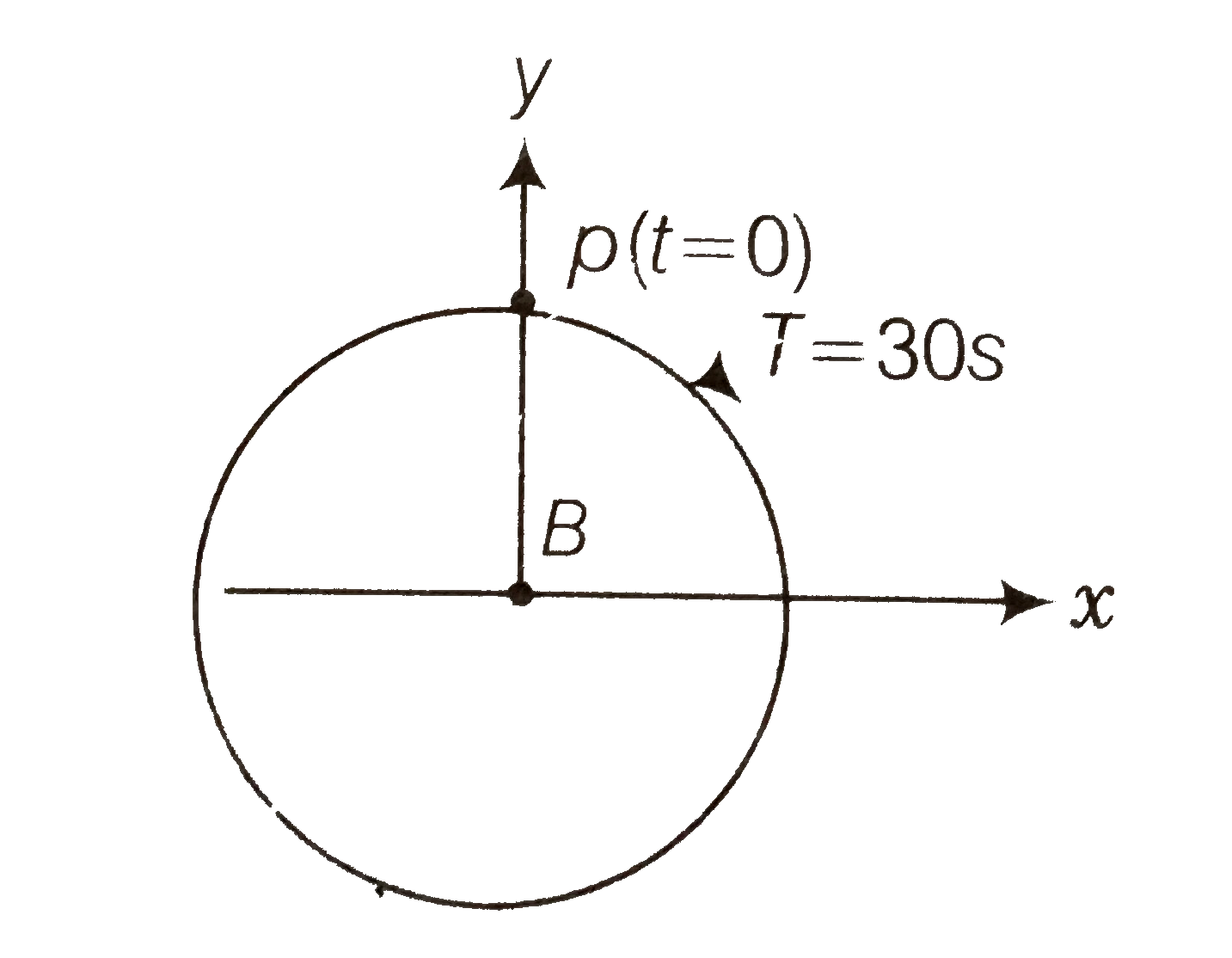
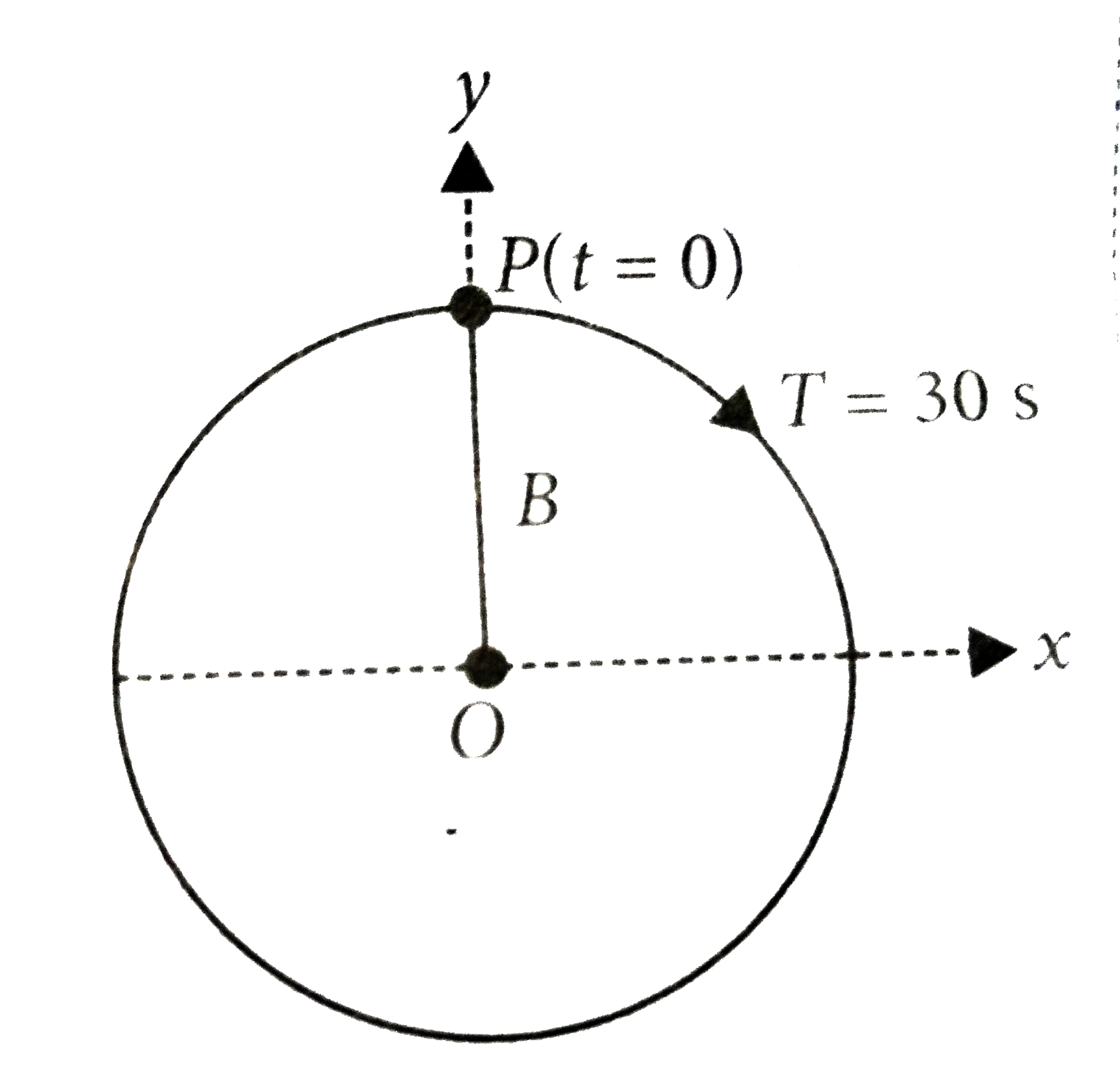
View SolutionFigure shows the circular motion of a particle. The radius of the circle, the period, same of revolution and the initial position are indicated on the figure. The simple harmonic motion of the x-projection of the radius vector the rotating particle P is
View SolutionA uniform disc of mass m and radius R is pivoted at point P and is free rotate in vertical plane. The centre C of disc is initially in horizontal position with P as shown in figure. If it is released from this position, then its angular acceleration when the line PC is inclined to the horizontal at an angle θ is
View SolutionA rod is rotating with a constant angular velocity ω about point O (its centre) in a magnetic field B as shown. Which of the folloiwng figure correctly shows the distribution of charge inside the rod?

View SolutionA uniform rod is hinged at its one end and is allowed to rotate in verticle plANE. Rod is given angular velocity ω in its verticle position as shown in figure. The value of ω for the force exerted by the hinge on rod is zero in this position is

View SolutionA solid sphere and a hollow sphere of equal mass and radius are placed over a rough horizontal surface after rotating it about its mass centre with same angular velocity ω0. Once the pure rolling starts let v1 and v2 be the linear speeds of their centres of mass. Then
View SolutionTorques of equal magnitude are applied to hollow cylinder and a solid sphere, both having the same mass and same radius. The cylinder is free to rotate about its standard axis of symmetry, and the sphere is free to rotate about an axis passing through its centre. which of the two will acquire a greater angular speed after a given time ?
View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What angle will the rod make with the vertical

View Solution
