Prove that the distances traversed during equal intervals of time by a body falling from rest, stand to one another in the same ratio as the odd numbers beginning with unity [namely 1: 3: 5: …………….].
To prove that the distances traversed during equal intervals of time by a body falling from rest stand to one another in the same ratio as the odd numbers beginning with unity (1: 3: 5: ...), we can follow these steps:
Step 1: Understanding the Problem
We need to find the distances traveled by a body falling freely under gravity during equal time intervals. The body starts from rest, so the initial velocity u=0.
Step 2: Using the Equation of Motion
For a body falling freely under gravity, the distance traveled in n seconds can be calculated using the equation:
Sn=ut+12gt2
Since the initial velocity u=0, this simplifies to:
Sn=12gn2
Step 3: Finding Distances in Each Interval
We need to find the distance traveled in each second interval:
- Distance traveled in the first second (S1):
S1=12g(1)2=12g
- Distance traveled in the second second (S2):
S2=12g(2)2=12g⋅4=2g
- Distance traveled in the third second (S3):
S3=12g(3)2=12g⋅9=92g
- Distance traveled in the fourth second (S4):
S4=12g(4)2=12g⋅16=8g
Step 4: Generalizing the Distance Formula
The distance traveled in the n-th second can be expressed as:
Sn=12g(n2)−12g((n−1)2)
This simplifies to:
Sn=12g(n2−(n2−2n+1))=12g(2n−1)
Step 5: Finding the Ratios
Now we can find the ratio of distances traveled in each second:
- For the 1st second: S1=12g(2⋅1−1)=12g
- For the 2nd second: S2=12g(2⋅2−1)=32g
- For the 3rd second: S3=12g(2⋅3−1)=52g
- For the 4th second: S4=12g(2⋅4−1)=72g
Step 6: Establishing the Ratio
The distances S1:S2:S3:S4 can be expressed as:
12g:32g:52g:72g
This simplifies to:
1:3:5:7
Conclusion
Thus, we have proved that the distances traversed during equal intervals of time by a body falling from rest stand to one another in the same ratio as the odd numbers beginning with unity (1: 3: 5: ...).
---
We need to find the distances traveled by a body falling freely under gravity during equal time intervals. The body starts from rest, so the initial velocity u=0.
For a body falling freely under gravity, the distance traveled in n seconds can be calculated using the equation:
Sn=ut+12gt2
Since the initial velocity u=0, this simplifies to:
Sn=12gn2
We need to find the distance traveled in each second interval:
- Distance traveled in the first second (S1):
S1=12g(1)2=12g
S2=12g(2)2=12g⋅4=2g
S3=12g(3)2=12g⋅9=92g
S4=12g(4)2=12g⋅16=8g
The distance traveled in the n-th second can be expressed as:
Sn=12g(n2)−12g((n−1)2)
This simplifies to:
Sn=12g(n2−(n2−2n+1))=12g(2n−1)
Now we can find the ratio of distances traveled in each second:
- For the 1st second: S1=12g(2⋅1−1)=12g
- For the 2nd second: S2=12g(2⋅2−1)=32g
- For the 3rd second: S3=12g(2⋅3−1)=52g
- For the 4th second: S4=12g(2⋅4−1)=72g
The distances S1:S2:S3:S4 can be expressed as:
12g:32g:52g:72g
This simplifies to:
1:3:5:7
Thus, we have proved that the distances traversed during equal intervals of time by a body falling from rest stand to one another in the same ratio as the odd numbers beginning with unity (1: 3: 5: ...).
Topper's Solved these Questions
Similar Questions
Galileo's law of odd number: The distances traversed, during equal intervals of time, by a body falling from rest, stand to one another in the same ratio as the odd number beginning with unity [namelly, 1:3:5:7....]. Prove it.
View SolutionA body starts from rest, what is the ratio of the distance travelled by the body during the 4th and 3rd s?
View Solution
Knowledge Check
When body slides down from rest along smooth inclined plane making angle of 45∘ with the horizontal, it takes time T When the same body slides down from rest along a rough inclined plane making the same angle and through the same distance it is seen to take time pT, where p is some number greater that 1. Calculate late the coefficient of friction beween the body and the rough plane.
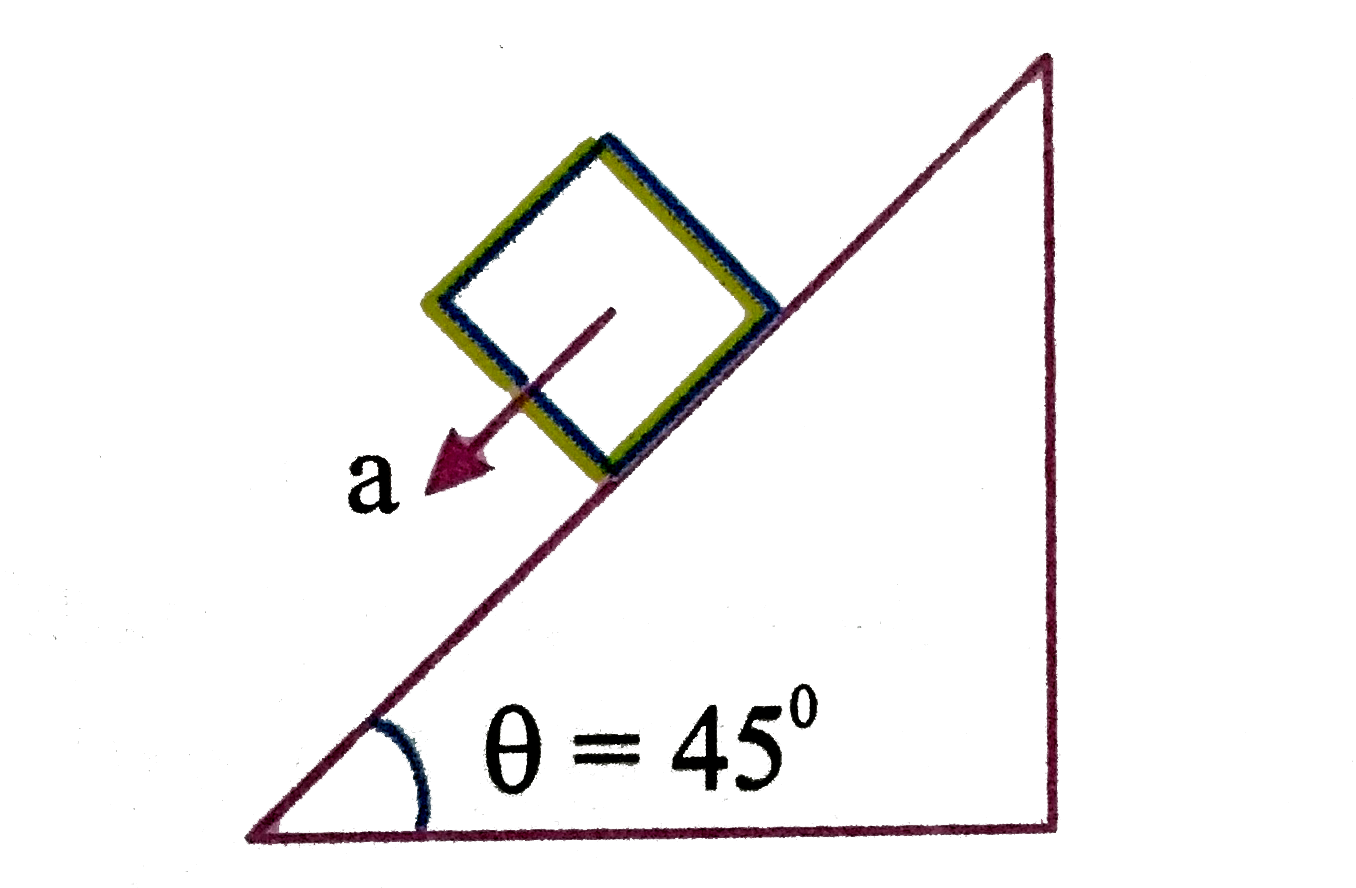 .A1/PBμ=(1−1/p2)C1/p2D2-p
.A1/PBμ=(1−1/p2)C1/p2D2-pWhen a body slides down from rest along a smooth inclined plane making an angle of 30∘ with the horizontal, it takes time 20s. When the same body slides down from rest along a rough inclined plane making the same angle and through the same distance, it takes time 20p is, where p is some number greater than 1. The coefficient of friction between the body and the rough plane is
Aμ=(1−1p2)1√3Bμ=(1−19p2)Cμ=(1−p2)1√3Dμ=√1−9p2
The distance moved by a freely falling body (startibg from rest) during st,2nd,3nd,……nth second of its motion are propotional to .
View SolutionA body falls for 5 s from rest. If the acceleration due to gravity of earth ceases to act, the distance it travels in the next 3 s is
View SolutionWhen body slides down from rest along smooth inclined plane making angle of 45∘ with the horizontal, it takes time T When the same body slides down from rest along a rough inclined plane making the same angle and through the same distance it is seen to take time pT, where p is some number greater that 1. Calculate late the coefficient of friction beween the body and the rough plane.
 .
.
View SolutionA particle of mass m and charge q is accelerated by a potential difference V volt and made to enter a magnetic field region at an angle θ with the field. At the same moment, another particle of same mass and charge is projected in the direction of the field from the same point. Magnetic field induction is B. What would be the speed of second particle so that both particles meet again and again after regular interval of time. Also, find the time interval after which they meet and the distance travelled by the second particle during that interval.
View SolutionA particle of mass m and charge q is accelerated by a potential difference V volt and made to enter a magnetic field region at an angle θ with the field. At the same moment, another particle of same mass and charge is projected in the direction of the field from the same point. Magnetic field induction is B. What would be the speed of second particle so that both particles meet again and again after regular interval of time. Also, find the time interval after which they meet and the distance travelled by the second particle during that interval.
View SolutionA proton is kept at rest. A positively charged particle is released from rest at a distance d in its field. Consider two experiments, one in which the charged particle is also a proton and in another, a positron. In the same time t, the work done on the two moving charged particles is
View Solution