A spherical capacitor consists of two concentric spherical conductors, held in position by suitable insulating supports. Show that the capacitance of this spherical capacitor is given by C=4π∈0r1r2r1−r2,
Where r1andr2 are radial of outer and inner spheres respectively.
To derive the capacitance of a spherical capacitor consisting of two concentric spherical conductors, we can follow these steps:
Step 1: Understanding the System
We have two concentric spherical conductors: an inner sphere with radius r2 and an outer sphere with radius r1. The inner sphere carries a charge −q, and the outer sphere, which is grounded, will have an induced charge of +q on its inner surface and will remain neutral overall.
Step 2: Define the Potential
The potential V at a distance r from a point charge is given by the formula:
V=14πϵ0qr
For our spherical capacitor, we need to calculate the potentials at the surfaces of both spheres.
Step 3: Potential of the Inner Sphere
The potential V2 at the surface of the inner sphere (radius r2) due to the charge −q is:
V2=14πϵ0−qr2
Step 4: Potential of the Outer Sphere
The potential V1 at the surface of the outer sphere (radius r1) due to the induced charge +q is:
V1=14πϵ0qr1
Step 5: Calculate the Potential Difference
The potential difference ΔV between the inner and outer spheres is given by:
ΔV=V2−V1=(−q4πϵ0r2)−(q4πϵ0r1)
Simplifying this, we get:
ΔV=−q4πϵ0(1r2+1r1)
This can be rewritten as:
ΔV=−q4πϵ0r1+r2r1r2
Step 6: Relating Charge and Capacitance
By definition, the capacitance C of a capacitor is given by:
C=qΔV
Substituting the expression for ΔV:
C=q−q4πϵ0r1+r2r1r2
This simplifies to:
C=4πϵ0r1r2r1−r2
Final Result
Thus, the capacitance of the spherical capacitor is given by:
C=4πϵ0r1r2r1−r2
We have two concentric spherical conductors: an inner sphere with radius r2 and an outer sphere with radius r1. The inner sphere carries a charge −q, and the outer sphere, which is grounded, will have an induced charge of +q on its inner surface and will remain neutral overall.
The potential V at a distance r from a point charge is given by the formula:
V=14πϵ0qr
For our spherical capacitor, we need to calculate the potentials at the surfaces of both spheres.
The potential V2 at the surface of the inner sphere (radius r2) due to the charge −q is:
V2=14πϵ0−qr2
The potential V1 at the surface of the outer sphere (radius r1) due to the induced charge +q is:
V1=14πϵ0qr1
The potential difference ΔV between the inner and outer spheres is given by:
ΔV=V2−V1=(−q4πϵ0r2)−(q4πϵ0r1)
Simplifying this, we get:
ΔV=−q4πϵ0(1r2+1r1)
This can be rewritten as:
ΔV=−q4πϵ0r1+r2r1r2
By definition, the capacitance C of a capacitor is given by:
C=qΔV
Substituting the expression for ΔV:
C=q−q4πϵ0r1+r2r1r2
This simplifies to:
C=4πϵ0r1r2r1−r2
Thus, the capacitance of the spherical capacitor is given by:
C=4πϵ0r1r2r1−r2
Topper's Solved these Questions
- BOOK - NCERT ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Exercise37videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NCERT ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise15videos
ELECTROMAGNETIC WAVES
- BOOK - NCERT ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Exercise25videos
MAGNETISM AND MATTER
Similar Questions
A spherical capacitor consists of two concentric spherical shells of outer radius r1 and inner radius r2, held in position by suitable insulating supports. calculate the capacitance of this spherical capacitor.
View SolutionThe capacitance of two concentric spherical shells of radii R1 and R2(R2>R1) is
View SolutionShow that (r1+r2)(r2+r3)(r3+r1)=4Rs2
View SolutionProve that r1r2+r2r3+r3r1=14(a+b+c)2
View SolutionShow that 16R2rr1r2r3=a2b2c2
View SolutionThe radii of two concentric spherical conducting shells are r1andr2(>r1). The change on the oute shell is q. The charge on the inner shell which is connected to the earth is
View SolutionFigure shows variation of acceleration due to gravity with distance from centre of a uniform spherical planet, Radius of planet is R. What is r1−r1
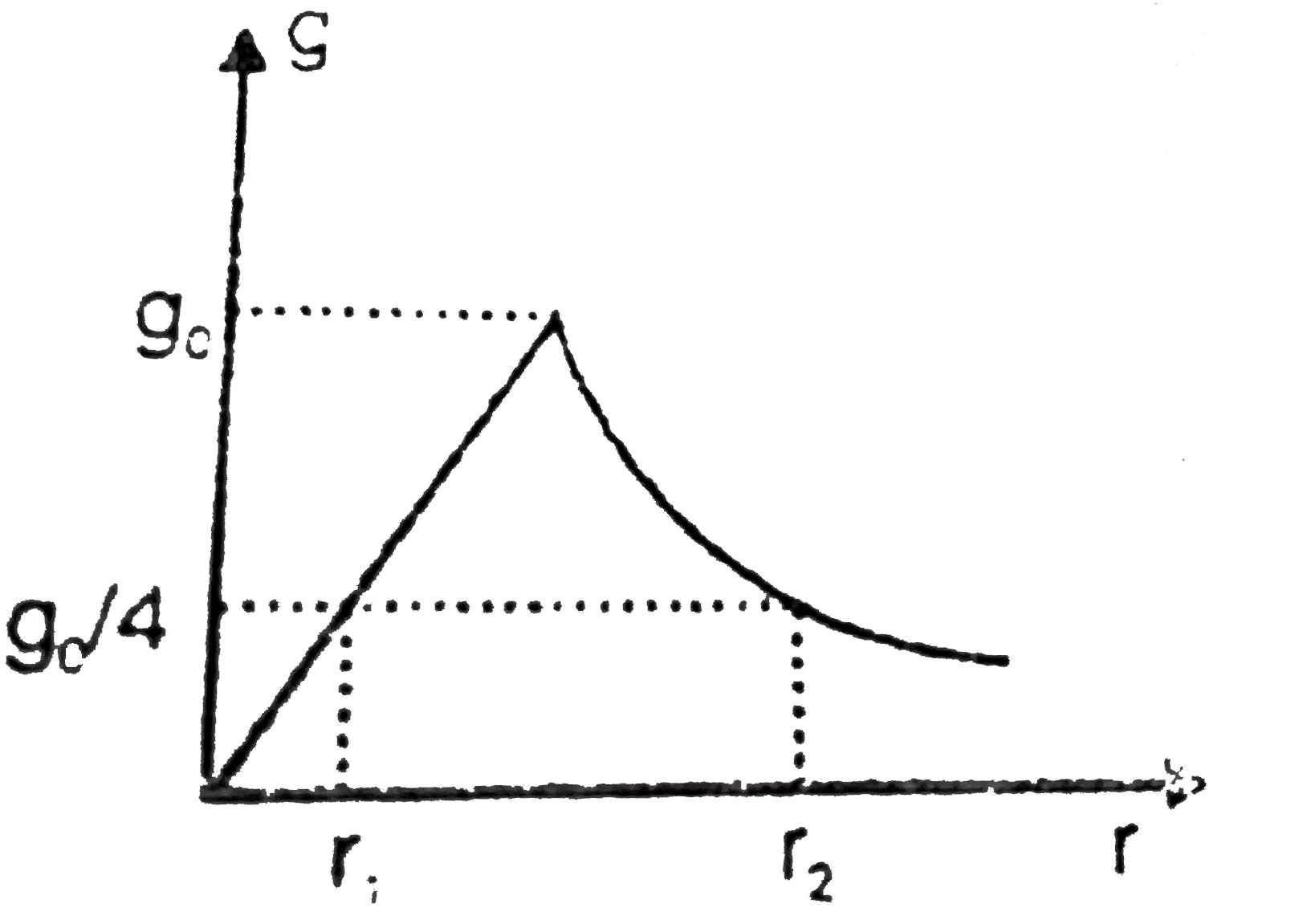 View Solution
View SolutionThree concentric spherical conductors A, B, and C of radii r, 2R, and 4R, respectively. A and C is shorted and B is uniformly charged (charge +Q).
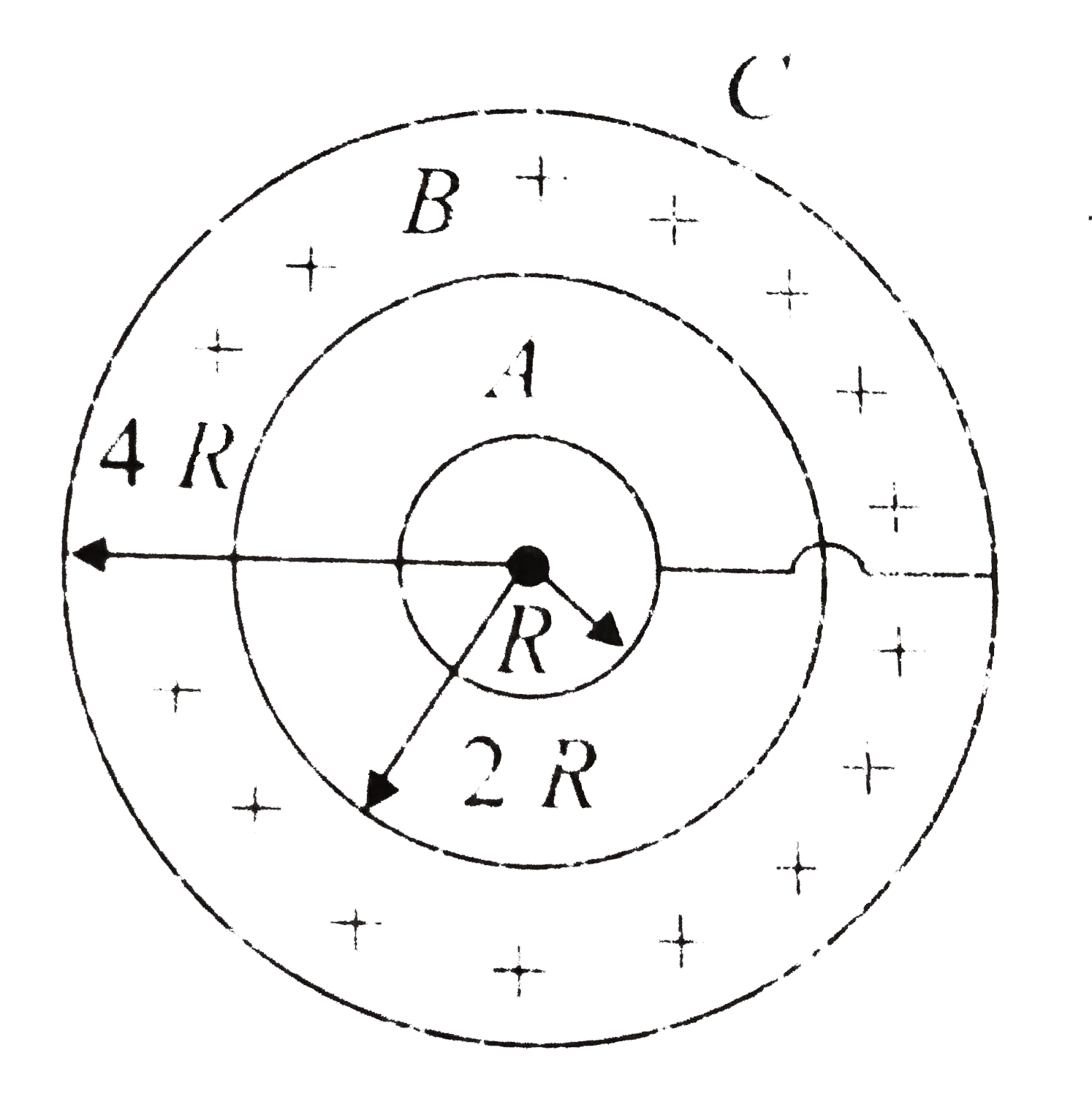
Potential at A isView SolutionThree concentric spherical conductors A, B, and C of radii r, 2R, and 4R, respectively. A and C is shorted and B is uniformly charged (charge +Q).
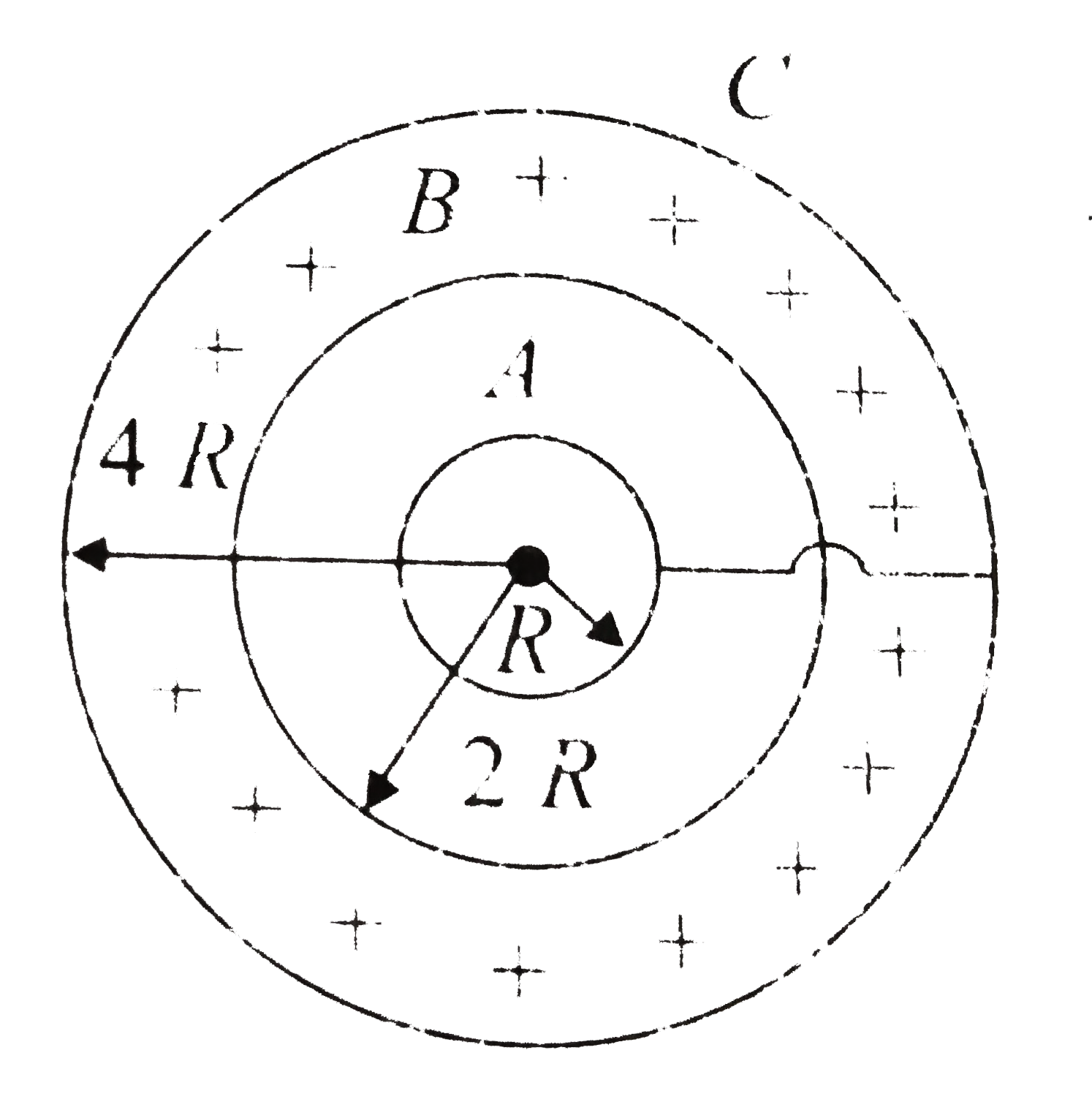
Potential at B isView SolutionA car is moving on a circular path and takes a turn. If R1 and R2 be the reactions on the inner and outer wheels, respectively, then
View Solution

