A small sphere of radius r1 and charge q1 is enclosed by a spherical shell of radius r2 and charge q2. Show that if q1 is positive, charge will necessarily flow from the sphere to the shell (when the two are connected by a wire) no matter what the charge q2 on the shell is [Fig]
To solve the problem, we need to analyze the electric potential at two points: one inside the sphere (point 1) and one on the surface of the shell (point 2). We will show that if the charge q1 on the sphere is positive, the charge will flow from the sphere to the shell when they are connected by a wire, regardless of the charge q2 on the shell.
1. Identify the Charges and Radii:
- Let the charge on the small sphere be q1 (which is positive).
- Let the charge on the spherical shell be q2.
- The radius of the small sphere is r1.
- The radius of the spherical shell is r2.
2. Calculate the Electric Potential at Point 1 (Inside the Sphere):
- The potential V1 at point 1 (inside the sphere) due to the charge q1 is given by:
V1=kq1r1
- The potential due to the charge q2 on the shell at this point (since it is inside the shell) is:
Vshell=kq2r2
- Therefore, the total potential at point 1 is:
V1=kq1r1+kq2r2
3. Calculate the Electric Potential at Point 2 (On the Surface of the Shell):
- The potential V2 at point 2 (on the surface of the shell) due to the charge q1 is:
V1,shell=kq1r2
- The potential due to the charge q2 on the shell at this point is also:
Vshell=kq2r2
- Therefore, the total potential at point 2 is:
V2=kq1r2+kq2r2
4. Compare the Potentials:
- We can compare V1 and V2:
V1=kq1r1+kq2r2
V2=kq1+q2r2
- Since r2>r1, we can see that:
V1>V2
- This shows that the potential at point 1 (inside the sphere) is greater than the potential at point 2 (on the surface of the shell).
5. Conclusion:
- When the sphere and the shell are connected by a wire, charge will flow from the higher potential (sphere) to the lower potential (shell).
- Therefore, charge will necessarily flow from the sphere to the shell when they are connected by a wire, regardless of the value of q2.
- Let the charge on the small sphere be q1 (which is positive).
- Let the charge on the spherical shell be q2.
- The radius of the small sphere is r1.
- The radius of the spherical shell is r2.
- The potential V1 at point 1 (inside the sphere) due to the charge q1 is given by:
V1=kq1r1
- The potential due to the charge q2 on the shell at this point (since it is inside the shell) is:
Vshell=kq2r2
- Therefore, the total potential at point 1 is:
V1=kq1r1+kq2r2
- The potential V2 at point 2 (on the surface of the shell) due to the charge q1 is:
V1,shell=kq1r2
- The potential due to the charge q2 on the shell at this point is also:
Vshell=kq2r2
- Therefore, the total potential at point 2 is:
V2=kq1r2+kq2r2
- We can compare V1 and V2:
V1=kq1r1+kq2r2
V2=kq1+q2r2
- Since r2>r1, we can see that:
V1>V2
- This shows that the potential at point 1 (inside the sphere) is greater than the potential at point 2 (on the surface of the shell).
- When the sphere and the shell are connected by a wire, charge will flow from the higher potential (sphere) to the lower potential (shell).
- Therefore, charge will necessarily flow from the sphere to the shell when they are connected by a wire, regardless of the value of q2.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NCERT ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Exercise
37 Videos
- ELECTROMAGNETIC WAVESBOOK - NCERT ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise
15 Videos
- MAGNETISM AND MATTERBOOK - NCERT ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Exercise
25 Videos
Similar Questions
A metal sphere A of radius a is charged to potential V. What will be its potential if it is enclosed by a spherical conducting shell B of radius b and the two are connected by a wire ?
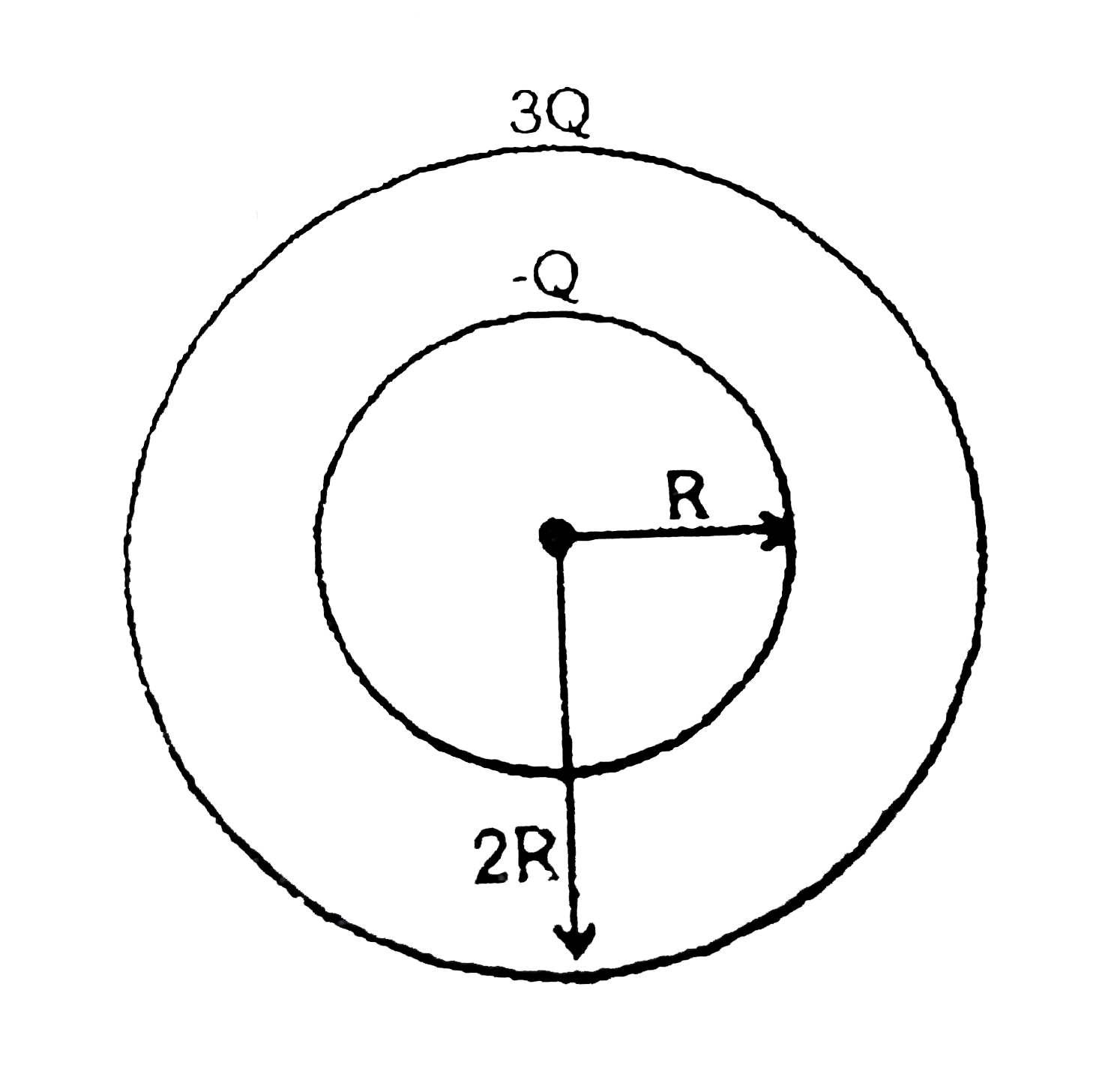
View SolutionTwo conducting hollow spherical shells of radius R and 2R carry charges -Q and 3Q respectively. How much charge will flow into the earth if inner shell is grounded?
View SolutionA solid conducting sphere of radius 10cm is enclosed by a thin metallic shell of radius 20cm. A charge q=20μC is given to the inner sphere is connected to the shell by a conducting wire.
View SolutionA solid metal sphere of radius R has a charg +2Q. A hollow spherical shell of radius 3R placed concentric with the frist sphere has net charge -Q.
What would be the final distribution of charges if the sphres are joined by a conducting wire
View SolutionConsider two concentric spherical metal shells of radii r1 and r2(r2>r1). If the outer shell has a charge q and the inner one is grounded, then the charge on the inner shell is
View SolutionA conducting sphere of radius R, carrying charge Q, lies inside uncharged conducting shell of radius 2R. If they are joined by a metal wire,
View SolutionA spherical shell of radius R1 with uniform charge q is expanded to a radius R2. Find the work performed by the electric forces in this process.
View SolutionA spherical shell of radius R is given charge 3q on its surface and a point charge q is placed at distance R/2 from its centre C. Also there is a charge 2q placed outside the shell at a distance of 2R as shown. Then

View SolutionA spherical conductor having charge q and radius r is placed at the centre of a spherical shell of radius R and having charge Q (R > r). The potential difference between the two is
View SolutionA spherical shell of radius R carries a uniformly distributed charge q. The electrical forces arising cause the ex-pansion of the shell. Find the mechanical stress in the shell.
View Solution
