An electrical technician requires a capacitance of in a circuit across a potential difference of 1 kV. A large number of capacitors are available to him each of which can withstand a potential difference of not more than 400 V. Suggest a possible arrangement that requires the minimum number of capacitors.
To solve the problem, we need to arrange the available 1 µF capacitors in such a way that we achieve a total capacitance of 2 µF while ensuring that the voltage across each capacitor does not exceed 400 V.
1. Determine the Voltage Requirement:
- The technician requires a potential difference of 1 kV (1000 V) across the capacitors.
- Each 1 µF capacitor can withstand a maximum of 400 V.
2. Calculate the Number of Capacitors in Series:
- To safely handle the 1000 V supply, we need to connect capacitors in series. The voltage across capacitors in series adds up.
- If each capacitor can withstand 400 V, the maximum number of capacitors (n) that can be connected in series is given by:
n=1000 V400 V=2.5
- Since we can only use whole capacitors, we round down to 2 capacitors in series. Thus, we will need at least 3 capacitors in series to safely handle the voltage.
3. Calculate the Equivalent Capacitance of Capacitors in Series:
- The formula for the equivalent capacitance Ceq of capacitors in series is:
1Ceq=1C1+1C2+1C3
- For 3 capacitors of 1 µF each:
1Ceq=11μF+11μF+11μF=31μF
- Therefore, the equivalent capacitance is:
Ceq=13μF≈0.333μF
4. Determine the Number of Rows Needed:
- To achieve a total capacitance of 2 µF, we need to connect multiple rows of these series capacitors in parallel.
- Let n be the number of rows of capacitors in parallel. The total capacitance Ctotal for capacitors in parallel is given by:
Ctotal=n⋅Ceq
- Setting Ctotal=2μF:
2μF=n⋅13μF
- Solving for n:
n=2μF⋅3=6
5. Final Arrangement:
- The technician needs to arrange 3 capacitors in series to handle the voltage, and then create 6 such rows in parallel.
- Therefore, the total number of capacitors required is:
Total capacitors=3 (in series)×6 (rows)=18 capacitors
Conclusion:
The technician should connect 3 capacitors of 1 µF in series to handle the voltage, and then connect 6 such series combinations in parallel to achieve a total capacitance of 2 µF. This arrangement requires a total of 18 capacitors.
- The technician requires a potential difference of 1 kV (1000 V) across the capacitors.
- Each 1 µF capacitor can withstand a maximum of 400 V.
- To safely handle the 1000 V supply, we need to connect capacitors in series. The voltage across capacitors in series adds up.
- If each capacitor can withstand 400 V, the maximum number of capacitors (n) that can be connected in series is given by:
n=1000 V400 V=2.5
- Since we can only use whole capacitors, we round down to 2 capacitors in series. Thus, we will need at least 3 capacitors in series to safely handle the voltage.
- The formula for the equivalent capacitance Ceq of capacitors in series is:
1Ceq=1C1+1C2+1C3
- For 3 capacitors of 1 µF each:
1Ceq=11μF+11μF+11μF=31μF
- Therefore, the equivalent capacitance is:
Ceq=13μF≈0.333μF
- To achieve a total capacitance of 2 µF, we need to connect multiple rows of these series capacitors in parallel.
- Let n be the number of rows of capacitors in parallel. The total capacitance Ctotal for capacitors in parallel is given by:
Ctotal=n⋅Ceq
- Setting Ctotal=2μF:
2μF=n⋅13μF
- Solving for n:
n=2μF⋅3=6
- The technician needs to arrange 3 capacitors in series to handle the voltage, and then create 6 such rows in parallel.
- Therefore, the total number of capacitors required is:
Total capacitors=3 (in series)×6 (rows)=18 capacitors
The technician should connect 3 capacitors of 1 µF in series to handle the voltage, and then connect 6 such series combinations in parallel to achieve a total capacitance of 2 µF. This arrangement requires a total of 18 capacitors.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NCERT ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Exercise
37 Videos
- ELECTROMAGNETIC WAVESBOOK - NCERT ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise
15 Videos
- MAGNETISM AND MATTERBOOK - NCERT ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Exercise
25 Videos
Similar Questions
A capacitance of 2μF is required in an electrical circuit across a potential difference of 1.0kV A large number of 1μF capacitors are available which can withstand a potential difference of not more than 300v.
The minimum number of capacitors required to achieve this is
View SolutionWhile working on a physics project at school physics, lab, you require a 4 μF capacitor in a circuit across a potential difference of 1 k V. Unfortunately, 4 μF capacitors are out or stock in your lab but 2 μF capacitors which can withstand a potential difference of 400 V are available in plenty . if you decide to use the 2 μF capacitors in place of 4μ F capacitor minimum number of capacitors required are
View SolutionIn the arrangement shown, a potential difference is applied between points A and B. No capacitor can withstand a potential difference of more than 100 V
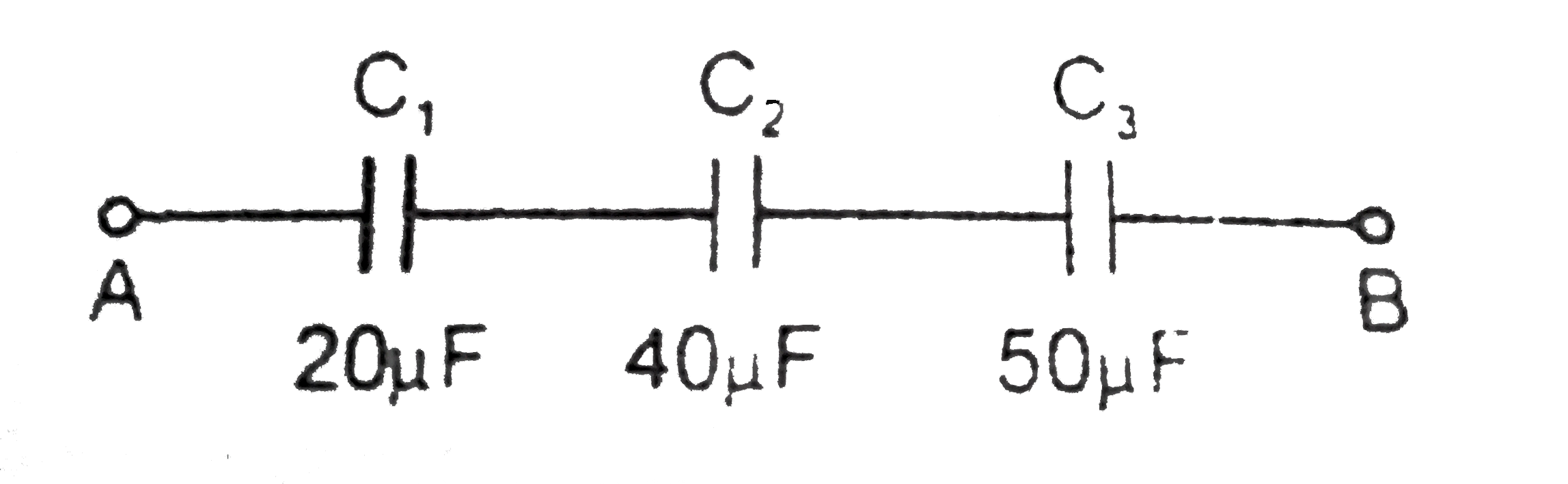
View SolutionIn the given circuit , the potential difference between A and B is 18 V and charge on 2 μF capacitor is 24 μ C . The value of C is

View SolutionA 100μF capacitor is charged to a potential difference of 24V. It is connected to an uncharged capacitor of capacitance 20μF What will be the new potential difference across the 100μF capacitor?
View SolutionSix 1μF capacitors are so arranged that their equivalent capacitance is 0.70μF. If a potential difference of 600 volt is applied to the combination, what charge will appear on each capacitor ?
View SolutionA capacitor of capacity 2μF is changed to a potential different of 12V . It is then connected across an inductor of inductance 0.6mH What is the current in the circuit at a time when the potential difference across the capacitor is 6.0V ?
View SolutionA capacitor of capacity 2μF is changed to a potential different of 12V . It is then connected across an inductor of inductance 0.6mH What is the current in the circuit at a time when the potential difference across the capacitor is 6.0V ?
View SolutionAn ideal capacitor of capacitance 0.2μF is charged to a potential difference of 10V. The charging battery is than disconnected. The capacitor is then connected to an ideal inductor of self inductance 0.5mH. The current at a time when the potential difference across the capacitor is 5V is :
View SolutionIn the given arrangement of the capacitors, one 3μF capacitor has got 600μJ of energy. Then the potential difference across 2μF capacitor is

View Solution
