A metal bar 70cm long and 4.00kg in mass is supported on two knife edges placed 10cm from each end. A 6.00kg weight is suspended at 30cm from one end. Find the reactions at the knife edges. Assume the bar to be of uniform cross-section and homogeneous.
To solve the problem, we need to find the reactions at the knife edges (N1 and N2) when a metal bar is supported at two points with an additional weight suspended from it. Here’s a step-by-step solution:
Step 1: Understand the System
- The metal bar is 70 cm long and has a mass of 4.00 kg.
- The bar's weight (W_bar) can be calculated using the formula:
Wbar=mass×g=4.00kg×9.81m/s2=39.24N
- The knife edges are placed 10 cm from each end, meaning they are located at 10 cm and 60 cm along the length of the bar.
- A 6.00 kg weight (W_weight) is suspended at 30 cm from one end, which can be calculated as:
Wweight=6.00kg×9.81m/s2=58.86N
Step 2: Set Up the Torque Equations
- Let N1 be the reaction at knife edge A (10 cm from the left end) and N2 be the reaction at knife edge B (60 cm from the left end).
- The center of mass of the bar is located at 35 cm from the left end (half of 70 cm).
- The distances from the knife edges to the center of mass and the weight are:
- Distance from A to the center of mass: 35cm−10cm=25cm
- Distance from A to the weight: 30cm−10cm=20cm
- Distance from B to the center of mass: 60cm−35cm=25cm
- Distance from B to the weight: 60cm−30cm=30cm
Step 3: Apply Torque Balance about Point A
- The sum of clockwise torques must equal the sum of counterclockwise torques.
- Clockwise torques due to weights:
Torquebar=Wbar×25cm=39.24N×0.25m=9.81Nm
Torqueweight=Wweight×20cm=58.86N×0.20m=11.772Nm
- Counterclockwise torque due to N2:
TorqueN2=N2×50cm=N2×0.50m
Setting up the equation:
9.81+11.772=N2×0.50
21.582=N2×0.50
N2=21.5820.50=43.164N
Step 4: Apply Torque Balance about Point B
- Now we apply torque balance about point B.
- Clockwise torque due to N1:
TorqueN1=N1×50cm=N1×0.50m
- Counterclockwise torques:
Torqueweight=Wweight×30cm=58.86N×0.30m=17.658Nm
Torquebar=Wbar×25cm=39.24N×0.25m=9.81Nm
Setting up the equation:
N1×0.50=17.658+9.81
N1×0.50=27.468
N1=27.4680.50=54.936N
Step 5: Final Results
- The reactions at the knife edges are:
- N1≈54.94N
- N2≈43.16N
- The metal bar is 70 cm long and has a mass of 4.00 kg.
- The bar's weight (W_bar) can be calculated using the formula:
Wbar=mass×g=4.00kg×9.81m/s2=39.24N
- The knife edges are placed 10 cm from each end, meaning they are located at 10 cm and 60 cm along the length of the bar.
- A 6.00 kg weight (W_weight) is suspended at 30 cm from one end, which can be calculated as:
Wweight=6.00kg×9.81m/s2=58.86N
- Let N1 be the reaction at knife edge A (10 cm from the left end) and N2 be the reaction at knife edge B (60 cm from the left end).
- The center of mass of the bar is located at 35 cm from the left end (half of 70 cm).
- The distances from the knife edges to the center of mass and the weight are:
- Distance from A to the center of mass: 35cm−10cm=25cm
- Distance from A to the weight: 30cm−10cm=20cm
- Distance from B to the center of mass: 60cm−35cm=25cm
- Distance from B to the weight: 60cm−30cm=30cm
- The sum of clockwise torques must equal the sum of counterclockwise torques.
- Clockwise torques due to weights:
Torquebar=Wbar×25cm=39.24N×0.25m=9.81Nm
Torqueweight=Wweight×20cm=58.86N×0.20m=11.772Nm
- Counterclockwise torque due to N2:
TorqueN2=N2×50cm=N2×0.50m
9.81+11.772=N2×0.50
21.582=N2×0.50
N2=21.5820.50=43.164N
- Now we apply torque balance about point B.
- Clockwise torque due to N1:
TorqueN1=N1×50cm=N1×0.50m
- Counterclockwise torques:
Torqueweight=Wweight×30cm=58.86N×0.30m=17.658Nm
Torquebar=Wbar×25cm=39.24N×0.25m=9.81Nm
N1×0.50=17.658+9.81
N1×0.50=27.468
N1=27.4680.50=54.936N
- The reactions at the knife edges are:
- N1≈54.94N
- N2≈43.16N
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - NCERT ENGLISHCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EXERCISE
33 Videos
- PHYSICAL WORLD BOOK - NCERT ENGLISHCHAPTER - PHYSICAL WORLD EXERCISE - EXERCISE
16 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXERCISE
22 Videos
Similar Questions
A metal rod of length 50cm having mass 2kg is supported on two edges placed 10cm from each end. A 3kg load is suspended at 20cm from one end. Find the reactions at the edges (take g=10m/s2)
View SolutionA metal rod of length 50cm having mass 2kg is supported on two edges placed 10cm from each end. A 3kg load is suspended at 20cm from one end. Find the reactions at the edges (take g=10m/s2)
View Solution
Knowledge Check
A uniform rod of length 1m mass 4kg is supports on tow knife-edges placed10cm from each end. A 60N weight is suspended at 30cm from one end. The reactions at the knife edges is.
Aa. 60 N, 40 NBb. 75 N, 25 NCc. 65 N, 35 NDd. 55 N, 45 NOne end of a uniform wire of length L and of weight W is attached rigidly to a point in the roof and a weight W1 is suspended from its lower end. IF S is the area of cross-section of the wire, the stress in the wire at a height 3L/4 from its lower end is
AW1/SB(W1+W4)SCW1+3W4SD(W1+W)S
A uniform half metre rule balances horizontally on a knife edge at 29 cm mark when a weight of 20 gf is suspended from one end.
What is the weight of the half metre rule ?
View SolutionA uniform half metre rule balances horizontally on a knife edge at 29 cm mark when a weight of 20 gf is suspended from one end.
Draw a diagram of the arrangement.
View SolutionA uniform metre rule between horizontally on a knife edge placed at the 58cm mark when a weight of 20gf is suspended from one end.
(i) Draw a diagram of the arrangement.
(ii) What is the weight of the rule?
View SolutionA diving board 3.00m long is supported at a point 1.00m from the end and a diver weighing 500N stands at the free end. The diving board is of uniform cross section and weighs 280N. Find.
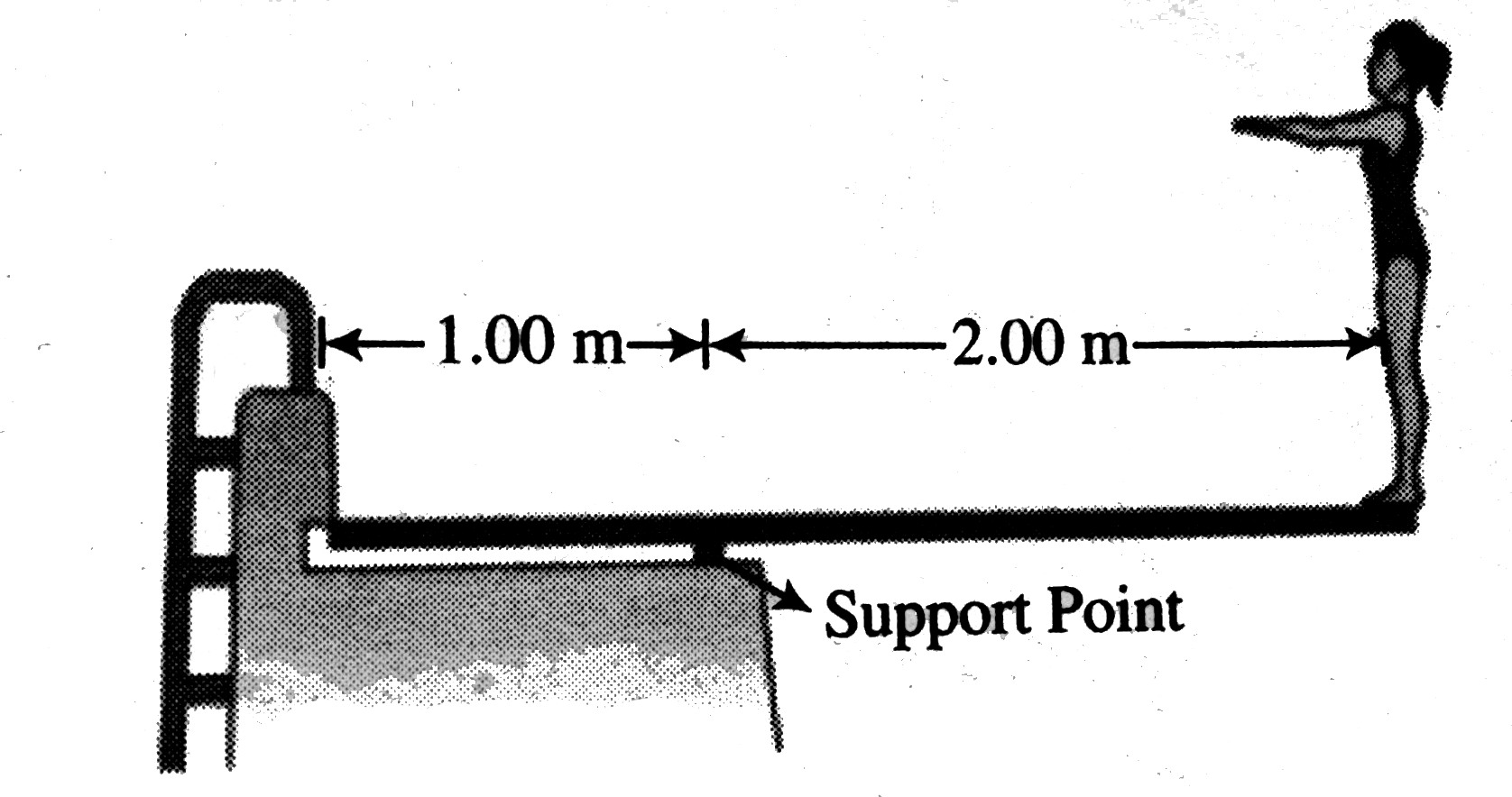
The force at the support point
View SolutionA diving board 3.00m long is supported at a point 1.00m from the end and a diver weighing 500N stands at the free end. The diving board is of uniform cross section and weighs 280N. Find.

The force at the end that is held down.
View SolutionTwo cubes each of 10cm edge are joined end to end. Find the surface area of the resulting cuboid.
View Solution
