Question

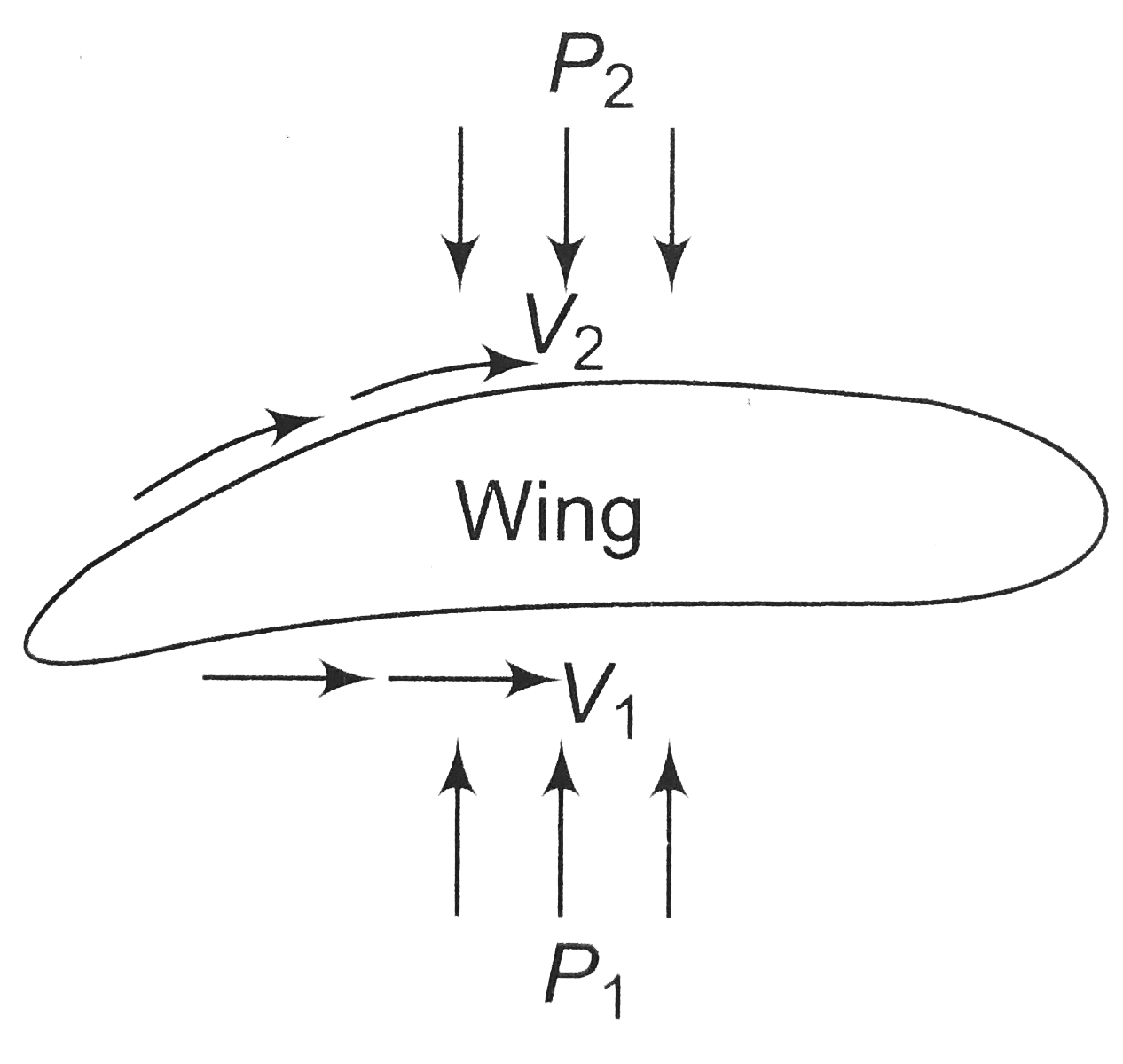
The speed of the wind passing over the wings of a small aeroplane is 70 m/s and below the wing is 60 m/s. If the mass of the plane is 1000 kg and the area of wing is $14m^2,$ then what will be ther net vertical force on the aeroplane ?
? (Density of air $=1.2kg/m^3\text{and}g=10m/s^2)$

Options

A. 2500 N
B. 5000 N
C. 1250 N
D. 7500 N

Answer

B

Explanation

To find the net vertical force on the aeroplane, we will follow these steps:

Step 1: Calculate the pressure difference using Bernoulli's principle.
According to Bernoulli's principle, the pressure difference between the upper and lower surfaces of the wing can be calculated using the formula:

\( P_2 - P_1 = \frac{1}{2} \rho (V_1^2 - V_2^2) \)

Where:
- \( \rho \) = density of air = 1.2 kg/m³
- \( V_1 \) = speed of air above the wing = 70 m/s
- \( V_2 \) = speed of air below the wing = 60 m/s

Substituting the values:

\( P_2 - P_1 = \frac{1}{2} \times 1.2 \times (70^2 - 60^2) \)

Calculating \( 70^2 \) and \( 60^2 \):

\( 70^2 = 4900 \quad \text{and} \quad 60^2 = 3600 \)

Thus,

\( P_2 - P_1 = \frac{1}{2} \times 1.2 \times (4900 - 3600) = \frac{1}{2} \times 1.2 \times 1300 \)

Calculating further:

\( P_2 - P_1 = 0.6 \times 1300 = 780 \text{ Pascals} \)

Step 2: Calculate the upward force due to pressure difference.
The upward force (thrust force) can be calculated using the pressure difference and the area of the wing:

\( F = (P_2 - P_1) \times A \)

Where:
- \( A \) = area of the wing = 14 m²

Substituting the values:

\( F = 780 \times 14 = 10920 \text{ Newtons} \)

Step 3: Calculate the weight of the aeroplane.
The weight of the aeroplane can be calculated using the formula:

\( W = m \times g \)

Where:
- \( m \) = mass of the aeroplane = 1000 kg
- \( g \) = acceleration due to gravity = 10 m/s²

Substituting the values:

\( W = 1000 \times 10 = 10000 \text{ Newtons} \)

Step 4: Calculate the net vertical force.
The net vertical force \( F_{net} \) acting on the aeroplane is the difference between the upward force and the weight of the aeroplane:

\( F_{net} = F - W \)

Substituting the values:

\( F_{net} = 10920 - 10000 = 920 \text{ Newtons} \)

Conclusion
The net vertical force on the aeroplane is 920 Newtons acting upwards.

---