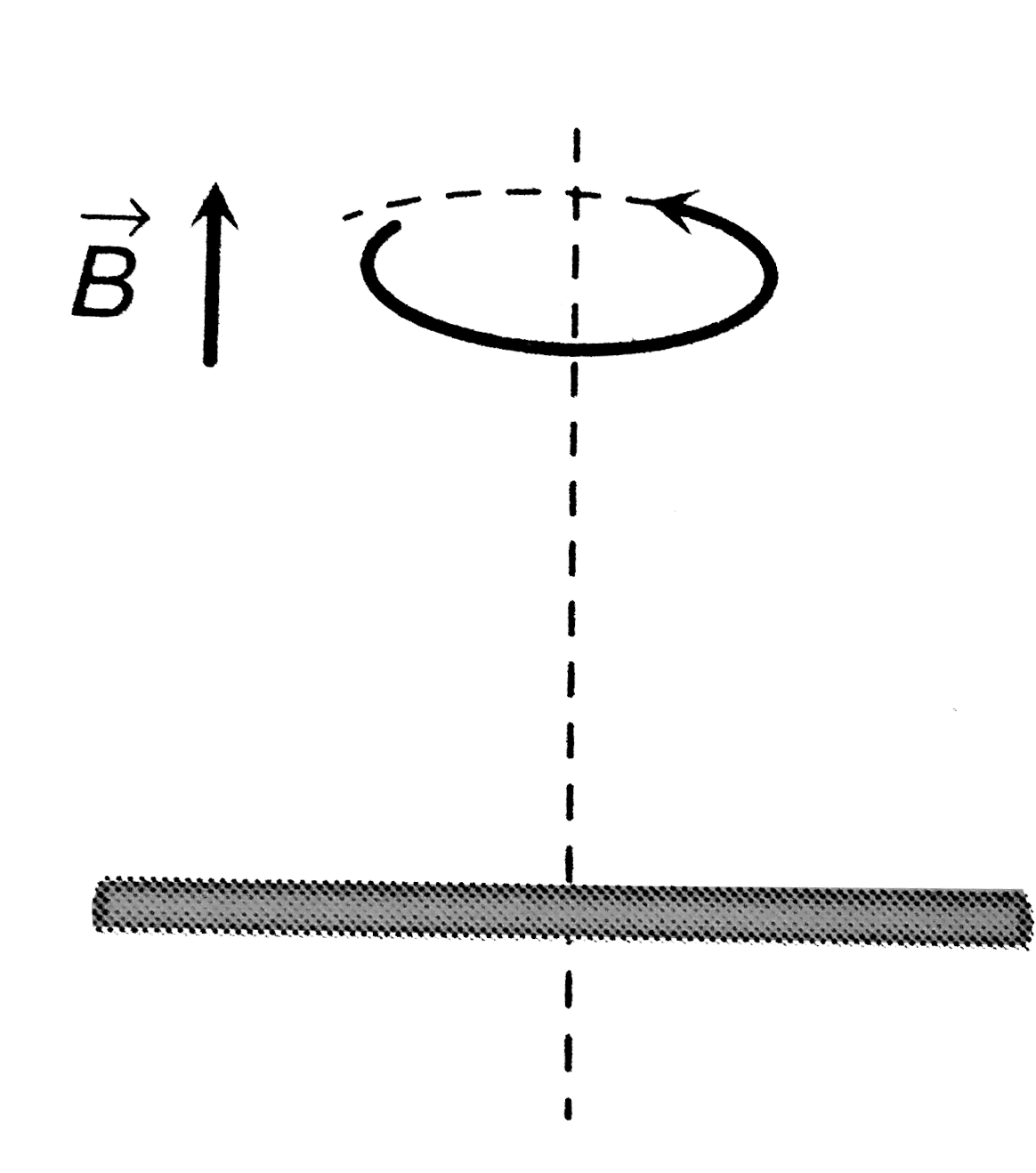
A 1m long calculating rod rotates with an angular frequency of 400 rad an axis normal to the rod passing through its one one end. The other end of the rod is contact with a circular metallic ring. A constant magnetic field of 0.5 T parallel to the axis everywhere. Calculate the e.m.f. developed between the centre and the ring.
To solve the problem of calculating the e.m.f. developed between the center and the ring of a rotating rod in a magnetic field, we can follow these steps:
Step 1: Identify the Given Values
- Length of the rod (L) = 1 m
- Angular frequency (ω) = 400 rad/s
- Magnetic field (B) = 0.5 T
Step 2: Determine the Average Velocity of the Rod
The average velocity (V_avg) of the end of the rod that is in contact with the ring can be calculated using the formula:
Vavg=12⋅ω⋅L
Substituting the known values:
Vavg=12⋅400rad/s⋅1m
Vavg=4002=200m/s
Step 3: Calculate the e.m.f. (Electromotive Force)
The e.m.f. (E) induced in the rod can be calculated using the formula:
E=B⋅L⋅Vavg
Substituting the values:
E=0.5T⋅1m⋅200m/s
E=0.5⋅200=100V
Final Answer
The e.m.f. developed between the center and the ring is 100 volts.
---
- Length of the rod (L) = 1 m
- Angular frequency (ω) = 400 rad/s
- Magnetic field (B) = 0.5 T
The average velocity (V_avg) of the end of the rod that is in contact with the ring can be calculated using the formula:
Vavg=12⋅ω⋅L
Vavg=12⋅400rad/s⋅1m
Vavg=4002=200m/s
The e.m.f. (E) induced in the rod can be calculated using the formula:
E=B⋅L⋅Vavg
E=0.5T⋅1m⋅200m/s
E=0.5⋅200=100V
The e.m.f. developed between the center and the ring is 100 volts.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - NCERT ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise
17 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Exercise
34 Videos
- ELECTROMAGNETIC WAVESBOOK - NCERT ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise
15 Videos
Similar Questions
A metallic rod of 1 m length is rotated with a frequency of 50 rev/s, with on end hinged at the centre and the other end at the circumference of a circular metallic ring of radius 1 m, about an axis passing through the centre and perpendicular at to the plane of the ring. A constant uniform magnetic field of 1 T parallel to the axis is persent eveywhere. what is the e.m.f. between the centre and the metallic ring?
View SolutionA metallic rod of 'L' length is rotated with angular frequency of 'w' with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius L, about an axis passing through the centre and perpendicular to the plane of the ring. A constant and uniform magnetic field B parallel to the axis is present everywhere. Deduce the expression for the emf between the centre and the metallic ring.
View Solution
Knowledge Check
A 2 m long metallic rod rotates with an angular frequency 200 rod s−1 about on axis normal to the rod passing through its one end. The other end of the rod is in contact with a circular metallic ring. A constant megnetic field of 0.5 T parallel to axis exises everywhere. The emf developed between the centre and the ring is
A100VB200VC300VD400VA metallic rod of 1 m length is rotated with a frequency of 50 rev/s, with on end hinged at the centre and the other end at the circumference of a circular metallic ring of radius 1 m, about an axis passing through the centre and perpendicular at to the plane of the ring. A constant uniform magnetic field of 1 T parallel to the axis is persent eveywhere. what is the e.m.f. between the centre and the metallic ring?
A157VB117VC127VD137V
A ring rotates with angular velocity ω about an axis perpendicula to the plane of the ring passing through the center of the ring (Fig. 3.77). A constant magnetic field B exists parallel to the axis. Find the emf induced in the ring.

View SolutionA metallic rod of length 'I' is rotated with a frequency v with one end hinged at the centre and the other end at the circumference of a circualr metallic ring of a radius r, about an axis passing through the centre and perpendicular to the plane of the ring. A constant uniform magnetic field B parallel to the axis is present every where. Using Lorentz force, explain how emf is induced between the centre and the metallic ring and hence obtain the expression for it.
View SolutionA rod of length 20 cm is rotating with angular speed of 100 rps in a magnetic field of strength 0.5 T about it’s one end . What is the potential difference betweet two ends of the rod :
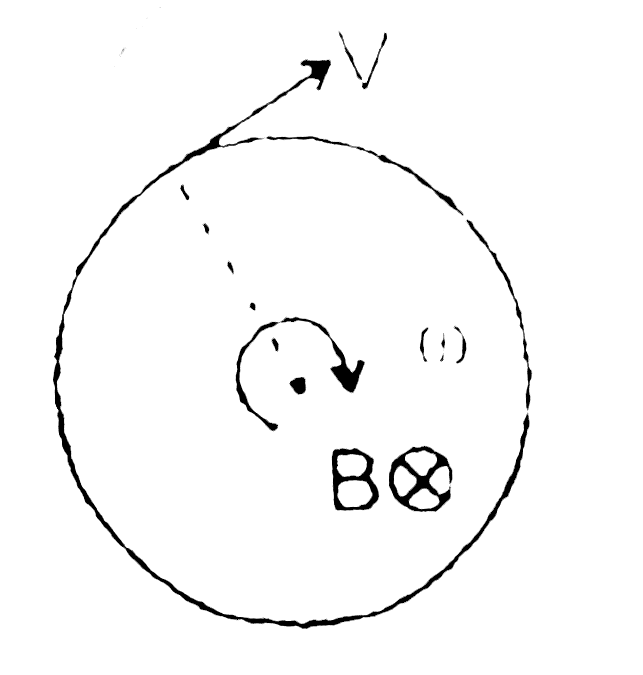
View SolutionA conducting rod of length 2l is rotating with constant angular speed w about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The e.m.f. induced between two ends of the rod is
View SolutionA conducting rod of length 2l is rotating with constant angular speed w about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The e.m.f. induced between two ends of the rod is

View SolutionA ring rotates with angular velocity ω about an axis perpendicular to the plane of the ring passing through the center of the ring.A constant magnetic field B exists parallel to the axis.Find the emf induced in the ring.
View Solution
