A rectangular loop of sides 8 cm and 2 cm with a small cut is moving out of a region of uniform megnetic field of magnitude 0.3 tesla directed normal to the loop. What is the voltage developed acorss the cut if velocity of the loop is 1cms−1 in a direction normal to the (i) longer side (ii) shorter side of the loop ? For how long does the induced voltage last in each case?
To solve the problem, we will follow these steps:
Given Data:
- Dimensions of the rectangular loop: Length L=8cm=0.08m, Width W=2cm=0.02m
- Magnetic field B=0.3T
- Velocity of the loop v=1cm/s=0.01m/s
(i) Case 1: Loop moving out normal to the longer side (8 cm side)
1. Calculate the EMF (E):
The formula for the induced EMF in a moving conductor in a magnetic field is given by:
E=B⋅L⋅v
Here, L is the length of the side of the loop that is perpendicular to the direction of motion. In this case, L=0.08m.
E=0.3T⋅0.08m⋅0.01m/s=2.4×10−4V
2. Calculate the time duration (t):
The time for which the induced EMF lasts can be calculated using the formula:
t=DistanceVelocity
The distance the loop moves out of the magnetic field is equal to the width of the loop, which is 0.02m.
t=0.02m0.01m/s=2s
(ii) Case 2: Loop moving out normal to the shorter side (2 cm side)
1. Calculate the EMF (E):
Using the same formula for EMF:
E=B⋅L⋅v
Here, L=0.02m (the shorter side).
E=0.3T⋅0.02m⋅0.01m/s=6×10−5V
2. Calculate the time duration (t):
The distance the loop moves out of the magnetic field is equal to the length of the loop, which is 0.08m.
t=0.08m0.01m/s=8s
Final Results:
- For the longer side (8 cm):
- Induced EMF E=2.4×10−4V
- Duration t=2s
- For the shorter side (2 cm):
- Induced EMF E=6×10−5V
- Duration t=8s
- Dimensions of the rectangular loop: Length L=8cm=0.08m, Width W=2cm=0.02m
- Magnetic field B=0.3T
- Velocity of the loop v=1cm/s=0.01m/s
The formula for the induced EMF in a moving conductor in a magnetic field is given by:
E=B⋅L⋅v
Here, L is the length of the side of the loop that is perpendicular to the direction of motion. In this case, L=0.08m.
E=0.3T⋅0.08m⋅0.01m/s=2.4×10−4V
The time for which the induced EMF lasts can be calculated using the formula:
t=DistanceVelocity
The distance the loop moves out of the magnetic field is equal to the width of the loop, which is 0.02m.
t=0.02m0.01m/s=2s
Using the same formula for EMF:
E=B⋅L⋅v
Here, L=0.02m (the shorter side).
E=0.3T⋅0.02m⋅0.01m/s=6×10−5V
The distance the loop moves out of the magnetic field is equal to the length of the loop, which is 0.08m.
t=0.08m0.01m/s=8s
- For the longer side (8 cm):
- Induced EMF E=2.4×10−4V
- Duration t=2s
- Induced EMF E=6×10−5V
- Duration t=8s
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - NCERT ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise
17 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Exercise
34 Videos
- ELECTROMAGNETIC WAVESBOOK - NCERT ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise
15 Videos
Similar Questions
A rectangular loop of sides 20 cm and 10 cm carries a current of 5.0 A. A uniform magnetic field of magnituded 0.20 T exists parallel ot the longer side of the loop (a) What is the force acting on the loop? (b) what is the torque acting on the loop?
View SolutionA square loop of sides 10cm carries a current of 10A.A uniform magnetic field of magnitude 0.20T exists parallel to one of the side of the loop.(a)What is the force acting on the loop? (b)What is the torque acting on the loop?
View Solution
Knowledge Check
A rectangular loop of sides 6 cm 2 cm with a samll cut is moving out of a region of uniform magnetic field of magnitude 0.4 T direction normal to the loop. The voltage developed acrss the cut if velocity of loop is 2cms−1 in a direction normal to the longer side is
A4.8×10−4VB1.6×10−4VC2.2×10−2VD3.2×10−2VIn the question number 40, if velocity is normal in the shorter side then voltage developed is
A2.3×10−4VB2.4×10−4VC4.8×10−2VD1.6×10−2V
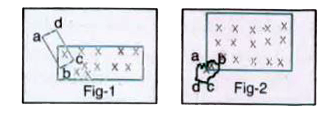
Figure shows planar loops of different shapes moving out of or into a region of a magnetic field which is directed normal to the plane of the loop away from the reader. Determine the direction of induced current in each loop using Lenz's law.

View SolutionFigures 1 and 2 show planar loops of different shapes moving out or into a region of magnetic field, which is directed normal to the plane of the loop and away for reader. Determine the direction of induced current
View SolutionA rectangular loop of sides 10 cm and 5 cm with a cut is stationary between the pole pieces of an electromagnet.
The magnetic field of the magnet is normal to the loop. The current feeding the electromagnet is reduced, so that the field decreased from its initial value of 0.2 T at the rate of 0.02Ω. If the cut is joined and the loop has a resistance of 2.0Ω, then the power dissipated by the loop as heat is
View SolutionA triangular loop of side l carries a current I. It is placed in a magnetic field B such that the plane of the loop is in the direction of B. The torque on the loop is
View SolutionA triangular loop of side l carries a current l. It is placed in a magnetic field B such that the plane of the loop is in the direction of B. The torque on the loop is
View SolutionA square loop of side 10 cm with its side parallel to X, and y axis is kept in a uniform magnetic field pointing towards positive z-direction. If magnetic field changes at the rate of 0.1 T/s, then induced emf is
View Solution