A square loop of side 12 cm with its sides parallel to X and Y axes is moved with a velocity of 8 cm s−1 in the positive x-direction in an environment containing a magnetic field in the positive z-direction. The field is neither uniform in space nor constant in time. It has a gradient of 10−3Tcm−1 along the negative x-direction (that is it increases by 10−3Tcm−1as one moves in the negative x-direction), and it is decreasing in time at the rate of 10−3Ts−1. Determine the direction and magnitude of the induced current in the loop if its resistance is 4.50 mΩ.
To solve the problem step by step, we will analyze the situation involving the square loop, the magnetic field, and the induced current.
Step 1: Understand the given parameters
- Side of the square loop (s): 12 cm = 0.12 m
- Velocity of the loop (v): 8 cm/s = 0.08 m/s
- Gradient of the magnetic field (dB/dx): 10−3T/cm=10−1T/m
- Rate of change of magnetic field with time (dB/dt): 10−3T/s
- Resistance of the loop (R): 4.5 mΩ = 4.5×10−3Ω
Step 2: Calculate the area of the loop
The area A of the square loop is given by:
A=s2=(0.12m)2=0.0144m2
Step 3: Calculate the change in magnetic flux due to the spatial gradient
The change in magnetic flux due to the spatial gradient of the magnetic field can be calculated using:
dΦdt=A⋅dBdx⋅v
Substituting the values:
dΦdt=0.0144m2⋅(10−1T/m)⋅(0.08m/s)=0.0144⋅0.1⋅0.08=1.152×10−5T m2/s
Step 4: Calculate the change in magnetic flux due to the time variation
The change in magnetic flux due to the time variation of the magnetic field is given by:
dΦdt=A⋅dBdt
Substituting the values:
dΦdt=0.0144m2⋅(10−3T/s)=1.44×10−5T m2/s
Step 5: Calculate the total induced EMF
The total induced EMF (E) is the sum of the contributions from both the spatial and temporal changes in magnetic flux:
E=dΦdt (spatial)+dΦdt (temporal)
Substituting the values:
E=1.152×10−5+1.44×10−5=2.592×10−5V
Step 6: Calculate the induced current
Using Ohm's Law, the induced current (I) can be calculated as:
I=ER
Substituting the values:
I=2.592×10−5V4.5×10−3Ω=5.76×10−3A=5.76mA
Step 7: Determine the direction of the induced current
To determine the direction of the induced current, we can use Lenz's Law, which states that the induced current will flow in a direction that opposes the change in magnetic flux. Since the magnetic field is decreasing in time, the induced current will flow in such a direction as to create a magnetic field in the same direction as the original field (positive z-direction).
Final Answer
- Magnitude of the induced current: 5.76mA
- Direction of the induced current: Counterclockwise (when viewed from above, in the positive z-direction).
- Side of the square loop (s): 12 cm = 0.12 m
- Velocity of the loop (v): 8 cm/s = 0.08 m/s
- Gradient of the magnetic field (dB/dx): 10−3T/cm=10−1T/m
- Rate of change of magnetic field with time (dB/dt): 10−3T/s
- Resistance of the loop (R): 4.5 mΩ = 4.5×10−3Ω
The area A of the square loop is given by:
A=s2=(0.12m)2=0.0144m2
The change in magnetic flux due to the spatial gradient of the magnetic field can be calculated using:
dΦdt=A⋅dBdx⋅v
Substituting the values:
dΦdt=0.0144m2⋅(10−1T/m)⋅(0.08m/s)=0.0144⋅0.1⋅0.08=1.152×10−5T m2/s
The change in magnetic flux due to the time variation of the magnetic field is given by:
dΦdt=A⋅dBdt
Substituting the values:
dΦdt=0.0144m2⋅(10−3T/s)=1.44×10−5T m2/s
The total induced EMF (E) is the sum of the contributions from both the spatial and temporal changes in magnetic flux:
E=dΦdt (spatial)+dΦdt (temporal)
Substituting the values:
E=1.152×10−5+1.44×10−5=2.592×10−5V
Using Ohm's Law, the induced current (I) can be calculated as:
I=ER
Substituting the values:
I=2.592×10−5V4.5×10−3Ω=5.76×10−3A=5.76mA
To determine the direction of the induced current, we can use Lenz's Law, which states that the induced current will flow in a direction that opposes the change in magnetic flux. Since the magnetic field is decreasing in time, the induced current will flow in such a direction as to create a magnetic field in the same direction as the original field (positive z-direction).
- Magnitude of the induced current: 5.76mA
- Direction of the induced current: Counterclockwise (when viewed from above, in the positive z-direction).
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - NCERT ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise
17 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Exercise
34 Videos
- ELECTROMAGNETIC WAVESBOOK - NCERT ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise
15 Videos
Similar Questions
A square loop of side 10 cm with its side parallel to X, and y axis is kept in a uniform magnetic field pointing towards positive z-direction. If magnetic field changes at the rate of 0.1 T/s, then induced emf is
View SolutionA conductor rod AB moves parallel to X-axis in a uniform magnetic field, pointing in the positive Z-direction. The end A of the rod gets-
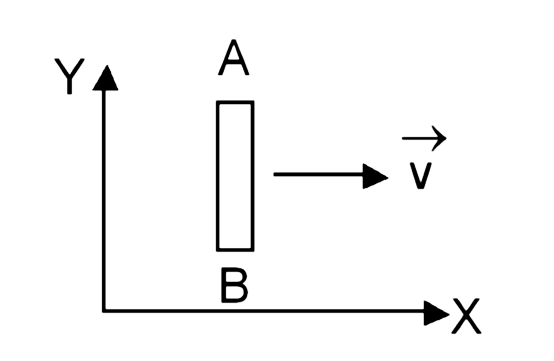
View SolutionAn electron having a charged e moves with a velcoity v in postive x direction. A magnetic field acts on it in positive y direction. The force on the electron acts in (where outward direction is taken as positive z-axis)
View SolutionA particle of mass m and charge q moves with a constant velocity v along the positive x direction. It enters a region containing a uniform magnetic field B directed along the negative z direction, extending from x=a to x=b. The minimum value of v required so that the particle can just enter the region x>b is
View SolutionA proton is moving along the negative direction of X-axis in a magnetic field directed along the positive direction of Y-axis. The proton will be deflected along the negative direction of
View SolutionAn electron is travelling along the x-direction. It encounters a magnetic field in the y-direction. Its subsequent motion will be
View SolutionAn electron is travelling along the x-direction. It encounters a magnetic field in the y-direction. Its subsequent motion wil be
View SolutionA conducting rod AB moves parallel to the x-axis (see Fig.) in a uniform magnetic field pointing in the positive z-direction. The end A of the rod gets positively charged.
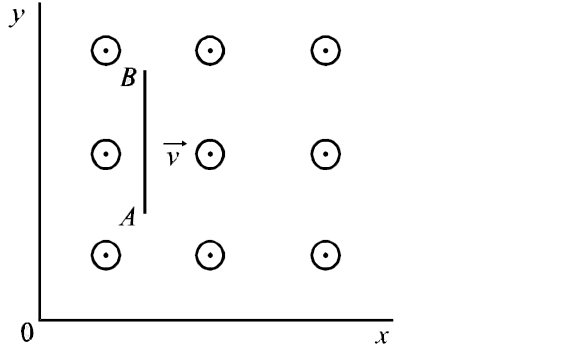 .
.
View SolutionA plane electromagnetic wave of frequency 28 MHz travels in free space along the positive x-direction . At a particular point in space and time, electric field is 9.3 V/m along positive y-direction. The magnetic field (in T) at that point is
View SolutionA charge moving with velocity V in X direction is subjected to a field of magnetic induction in the negative X direction . As a result the charge will
View Solution
