A charged metallic sphere A is suspended by a nylon thread. Another charged metallic sphere B held by an insulating handle is brought close to A such that the distance between their centres is 10 cm, as shown in Fig. 1.7(a). The resulting repulsion of A is noted (for example, by shining a beam of light and measuring the deflection of its shadow on a screen). Spheres A and B are touched by uncharged spheres C and D respectively, as shown in Fig. 1.7(b). C and D are then removed and B is brought closer to A to a distance of 5.0 cm between their centres, as shown in Fig. 1.7(c). What is the expected repulsion of A on the basis of Coulomb’s law? Spheres A and C and spheres B and D have identical sizes. Ignore the sizes of A and B in comparison to the separation between their centres.
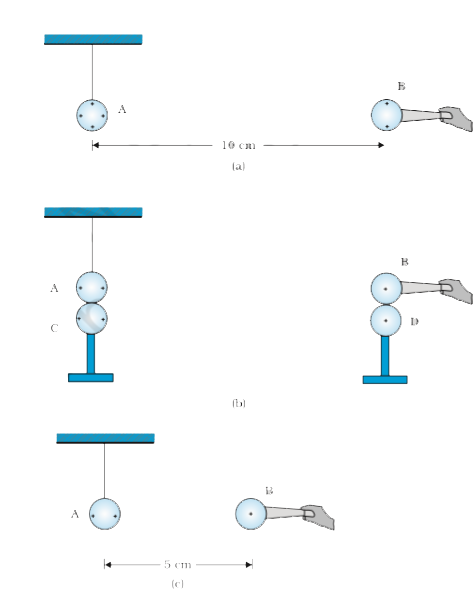
Let the original charge on sphere A be q and that on B be q′. At a distance r between their centres, the magnitude of the electrostatic force on each is given by
neglecting the sizes of spheres A and B in comparison to r. When an identical but uncharged sphere C touches A, the charges redistribute on A and C and, by symmetry, each sphere carries a charge q/2. Similarly, after D touches B, the redistributed charge on each is q′/2. Now, if the separation between A and B is halved, the magnitude of the electrostatic force on each is
Thus the electrostatic force on A, due to B, remains unaltered.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Exercise
34 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - NCERT ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - All Questions
32 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - NCERT ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise
17 Videos
Similar Questions
One metallic sphere A is given positive charge whereas another identical metallic sphere B of exactly same mass as of A is given equal amount of negative charge. Then
View SolutionA metal sphere is suspended from a nylon thread. Initially, the metal sphere is uncharged. When a positively charged glass rod is brought close to the metal sphere, the sphere is drawn towards the rod. But if the sphere touches the rod, it suddenly flies away from the rod. Explain, why the sphere is first attracted then repelled?
View Solution
Knowledge Check
Metallic sphere of radius R is charged to potential V. Then charge q is proportional to
AVBRCboth V and RDnone of these
A hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
View SolutionA small conducting sphere is hanged by an insulating thread between the plates of a parallel plate capacitor as shown in figure. The net force on the sphere is
View SolutionA small elecrtrically charged sphere is suspended vertically from a thread. An oppositely charged rod is brought close to the sphere such that the sphere is the sphere is in equlibrium displaced from the vertical by an angle of 30∘. When one of the following best represents the free body diagram for the sphere?
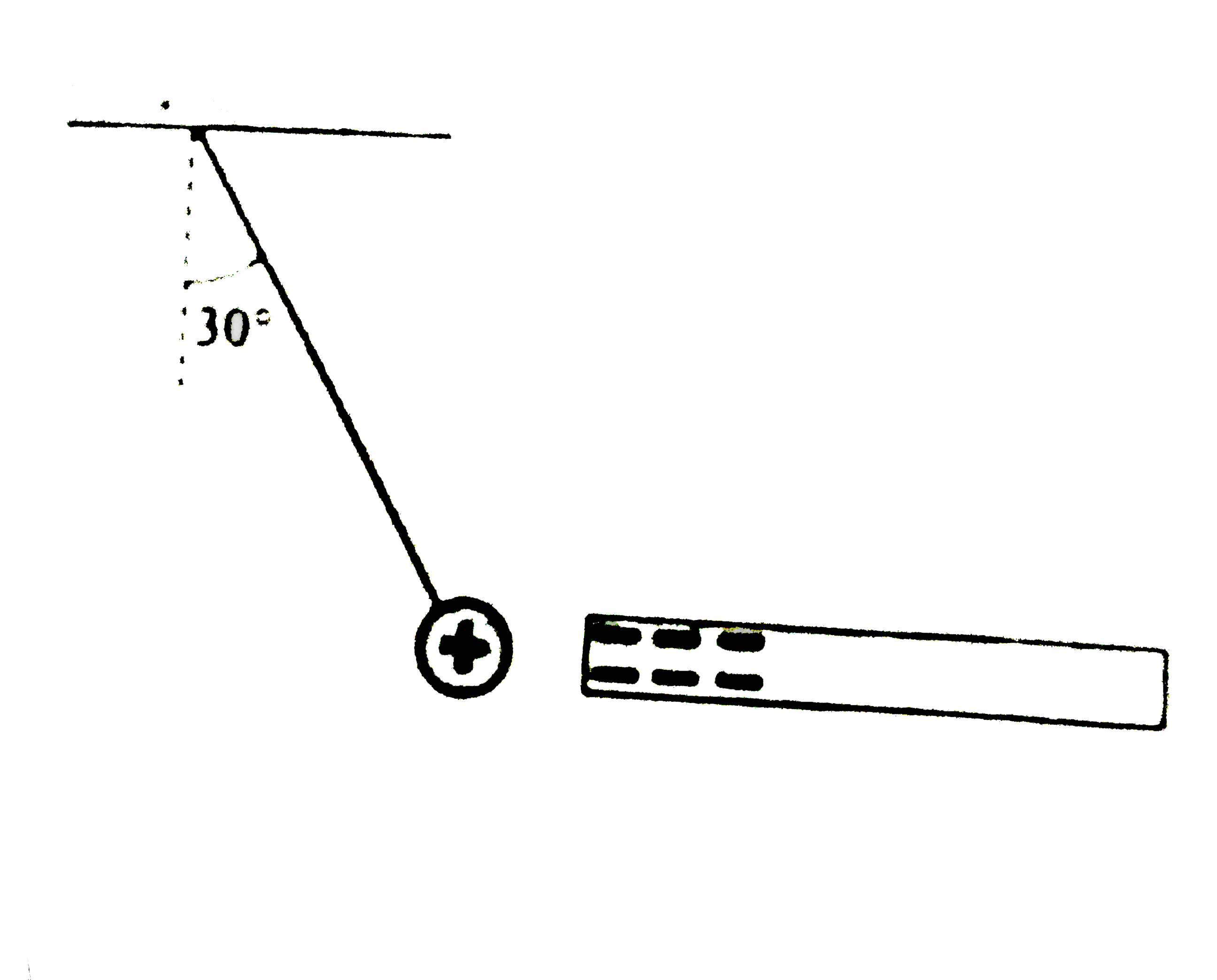
View SolutionAn uncharged metal sphere suspended by a silk thread is placed in a uniform extermal electric field. E. (a) what is the magnitude of the electric field for points inside the sphere ? (b) is your answer changed if the sphere carriers a charge ?
View SolutionA sphere of 4cm radius is suspended within a hollow sphere of 6cm radius. The inner sphere is charged to potential 3 e.s.u. and the outer sphere is earthed. The charge on the inner sphere is
View SolutionA sphere of 4cm radius is suspended within a hollow sphere of 6cm radius. The inner sphere is charged to potential 3 e.s.u. and the outer sphere is earthed. The charge on the inner sphere is
View SolutionA conducting sphere of radius 10cm is charged 10μC. Another uncharged sphere of radius 20cm is allowed to touch it for some tome. After that if the sphere are separted, then surface density of chsrges, on the spheres will be in the ratio of
View Solution
