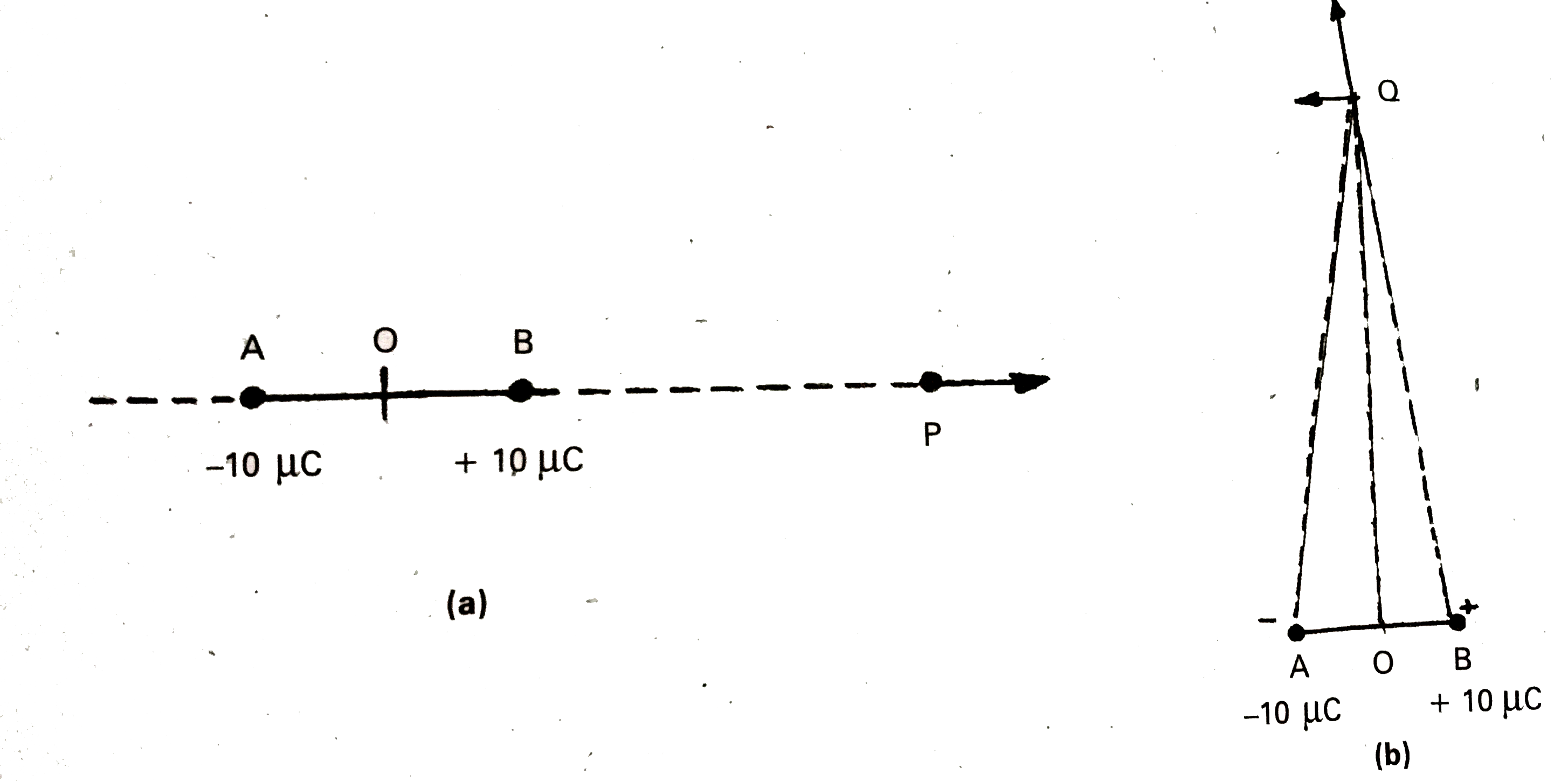
Two charges ±10μC are placed 5⋅0mm apart. Determine the electric field at (a) point P on the axis of dipole 15cm away from its center on the side of the positive charge. As shown in Figure and at (b) a point Q. 15cm away form O on a line passing through O and a line passing through O and normal to the axis of the dipole as shown in Fig.
Two charges +- 10 mu C are placed 5*0 mm apart. Determine the electric field at (a) point P on the axis of dipole 15 cm away from its center on the side of the positive charge. As shown in Figure and at (b) a point Q. 15 cm away form O on a line passing through O and a line passing through O and normal to the axis of the dipole as shown in Fig.

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

(a) Field at P due to charge +10μC
=108C4π(8.854×10−12C2N−1m−2)×1(15−0.25)3×10−4m3
=4.13×108NC−1along BP
Field at P due to charge −10μC
=108C4π(8.854×10−12C2N−1m−2)×1(15−0.25)3×10−4m3
The resultant electric field at P due to the two charges at A and B is
=2.7×105NC−1along BP.
In this example, the ratio OP/OB is quite large (= 60). Thus, we canexpect to get approximately the same result as above by directly usingthe formula for electric field at a far-away point on the axis of a dipole.For a dipole consisting of charges ± q, 2a distance apart, the electricfield at a distance r from the centre on the axis of the dipole has amagnitude
E=24πε0r3 (r/a>>1)
where p = 2a q is the magnitude of the dipole moment. The direction of electric field on the dipole axis is always along thedirection of the dipole moment vector (i.e., from –q to q).
Here,p=10−5C×5×10−3m=5×10−8Cm
Therefore
=108C4π(8.854×10−12C2N−1m−2)×1(15)3×10−4m3=2.6×105NC−1
along the dipole moment direction AB, which is close to the result obtained earlier.
(b) Field at Q due to charge +10μCatB
=105C4π(8.854×10−12C2N−1m−2)×1[152−(0.25)3]×10−4m2
=3.99×106NC−1along BQ ltBRgt Field at Q due to charge −10μCatA
=108C4π(8.854×10−12C2N−1m−2)×1[152−(0.25)3]×10−4m3
=3.99×106NC−1along QA.
Clearly, the components of these two forces with equal magnitudes cancel along the direction OQ but add up along the direction parallel to BA. Therefore, the resultant electric field at Q due to the two charges at A and B is =2×0.25√152+(0.25)2=3.99×106NC−1along BA
1.33×105NC−1along BAAs in (a), we can expect to get approximately the same result by directly using the formula for dipole field at a point on the normal to the axis of the dipole:
E=P4πε0r3 (r/a>>1)
=5×108Cm4π(8.854×10−12C2N−1m−2)×1(15)3×10−6m3
=1.33×105NC−1
The direction of electric field in this case is opposite to the direction of the dipole moment vector. Again, the result agrees with that obtained before.

Updated on:21/07/2023
|
Class 12PHYSICSELECTROSTATICS

Topper's Solved these Questions

Similar Questions