A pump on the ground floor of a building can pump of water to fill a tank of volume in . If the tank is above the ground and the efficiency of the pump is , how much electric power is consumed by the pump?
To solve the problem, we need to calculate the electric power consumed by the pump. We will follow these steps:
Step 1: Calculate the mass of water
The mass of water can be calculated using the formula:
mass=density×volume
Given:
- Density of water, ρ=1000kg/m3
- Volume of water, V=30m3
So,
mass=1000kg/m3×30m3=30000kg
Step 2: Calculate the change in potential energy
The change in potential energy (ΔPE) can be calculated using the formula:
ΔPE=mgh
Where:
- m=30000kg (mass of water from Step 1)
- g=10m/s2 (acceleration due to gravity)
- h=40m (height of the tank)
So,
ΔPE=30000kg×10m/s2×40m=12000000J
Step 3: Calculate the output power of the pump
Output power (Po) can be calculated using the formula:
Po=ΔPEtime
Given that the time taken is 15 minutes, we convert this to seconds:
time=15minutes×60seconds/minute=900s
Now, substituting the values:
Po=12000000J900s=13333.33W
Step 4: Calculate the input power of the pump
Given the efficiency (η) of the pump is 30%, we can use the formula:
η=PoPi
Rearranging gives us:
Pi=Poη
Converting the efficiency to decimal:
η=0.30
Now substituting the values:
Pi=13333.33W0.30=44444.44W
Step 5: Convert to kilowatts
To convert watts to kilowatts:
Pi=44444.44W1000=44.44kW
Final Answer
The electric power consumed by the pump is approximately 44.44 kW.
---
The mass of water can be calculated using the formula:
mass=density×volume
- Density of water, ρ=1000kg/m3
- Volume of water, V=30m3
mass=1000kg/m3×30m3=30000kg
The change in potential energy (ΔPE) can be calculated using the formula:
ΔPE=mgh
- m=30000kg (mass of water from Step 1)
- g=10m/s2 (acceleration due to gravity)
- h=40m (height of the tank)
ΔPE=30000kg×10m/s2×40m=12000000J
Output power (Po) can be calculated using the formula:
Po=ΔPEtime
time=15minutes×60seconds/minute=900s
Po=12000000J900s=13333.33W
Given the efficiency (η) of the pump is 30%, we can use the formula:
η=PoPi
Pi=Poη
η=0.30
Pi=13333.33W0.30=44444.44W
To convert watts to kilowatts:
Pi=44444.44W1000=44.44kW
The electric power consumed by the pump is approximately 44.44 kW.
Topper's Solved these Questions
Similar Questions
A pump on the ground floor of a building can pump up water to fill a tank of volume 30m3 in 15 min. If the tank is 60 m above the ground, and the efficiency of the pump is 40%, how much electric power is consumed by the pump?
(Take g=10ms−2)
View SolutionAn electric pump on the ground floor of a building taken 10 minute to fill a tank of 45m3 with water. The tank is 20m above the water level . If electric power consumed by the pump is 30kW then efficiency of the pump will be ( density of water is 1000kgm3)
View SolutionAn engine pumps up 100kg water through a height of 10m in 5s. If efficiency of the engine is 60%. What is the power of the engine? Takeg=10ms2.
View SolutionThe power of a motor pump is 2kW. How much water per minute the pump can raise to a heiht of 10 m ? (Given g=10m/s2)
View SolutionA ball is thrown vertically upwards from the ground and a student gazing out of the window sees it moving upward past him at 10ms−1. The window is at 15 m above the ground level. The velocity of ball 3 s after it was projected from the ground is [Take g=10ms−2]
View SolutionAn engine pumps 400 kg of water through height of 10 m in 40 s. Find the power of the engine if its efficiency is 80% (Take ,g =10 ms−2).
View SolutionAn engine pumps 400 kg of water through height of 10 m in 40 s. Find the power of the engine if its efficiency is 80% (Take ,g =10 ms−2).
View SolutionAn engine pumps 400 kg of water through height of 10 m in 40 s. Find the power of the engine if its efficiency is 80% (Take ,g =10 ms−2).
View SolutionAn engine pumps 800 kg of water through height of 10 m in 80 s. Find the power of the engine if its efficiency is 75%
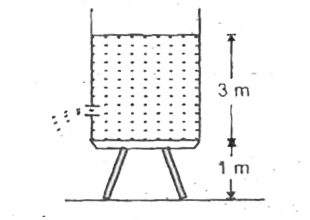
View SolutionWater is filled in a tank upto 3 m height. The base of the tank is at height 1 m above the ground. What should be the height of a hole made in it, so that water can be sprayed upto maximum horizontal distance on ground?
View Solution
