A series L-C-R circuit with R = 20Ω, L = 1.5 H and C =35μF is connected to a variable frequency 200 V, AC supply. When the frequency of the supply equals the natural frequency of the circuit, what is the average power transfered to the circuit, what is the average power transfered to the circuit in one complete cycle ?
To solve the problem step by step, we will follow the principles of an L-C-R circuit at resonance.
Step 1: Identify the given values
- Resistance (R) = 20 Ω
- Inductance (L) = 1.5 H
- Capacitance (C) = 35 µF = 35 × 10^(-6) F
- Voltage (V_rms) = 200 V
Step 2: Determine the natural frequency (ω₀) of the circuit
The natural frequency of a series L-C-R circuit is given by the formula:
ω0=1√LC
Substituting the values of L and C:
ω0=1√1.5×35×10−6
Step 3: Calculate the impedance (Z) at resonance
At resonance, the impedance (Z) of the circuit is equal to the resistance (R):
Z=R=20Ω
Step 4: Calculate the RMS current (I_rms)
The RMS current can be calculated using Ohm's law for AC circuits:
Irms=VrmsZ
Substituting the values:
Irms=20020=10A
Step 5: Calculate the average power (P)
The average power transferred to the circuit in one complete cycle is given by:
P=Vrms×Irms×cos(ϕ)
At resonance, the phase angle (φ) is 0, hence cos(φ) = 1. Thus:
P=200×10×1=2000W=2kW
Conclusion
The average power transferred to the circuit in one complete cycle is 2 kW.
---
- Resistance (R) = 20 Ω
- Inductance (L) = 1.5 H
- Capacitance (C) = 35 µF = 35 × 10^(-6) F
- Voltage (V_rms) = 200 V
The natural frequency of a series L-C-R circuit is given by the formula:
ω0=1√LC
Substituting the values of L and C:
ω0=1√1.5×35×10−6
At resonance, the impedance (Z) of the circuit is equal to the resistance (R):
Z=R=20Ω
The RMS current can be calculated using Ohm's law for AC circuits:
Irms=VrmsZ
Substituting the values:
Irms=20020=10A
The average power transferred to the circuit in one complete cycle is given by:
P=Vrms×Irms×cos(ϕ)
At resonance, the phase angle (φ) is 0, hence cos(φ) = 1. Thus:
P=200×10×1=2000W=2kW
The average power transferred to the circuit in one complete cycle is 2 kW.
Similar Questions
A series LCR circuit with R=20Ω,L=1.5H and C=35μF is connected to a variable frequency 200V ac supply. When the frequency of the supply equals the natural frequency of the circuit, what is the average power in kW transferred to the circuit in one complete cycle?
View SolutionA series LCR circuit with L=0.12H,C=480nF, and R=23Ω is connected to a 230V variable frequency supply.
(a) What is the source frequency for which current amplitude is maximum? Find this maximum value.
(b) What is the source frequency for which average power absorbed by the circuit is maximum? Obtain the value of maximum power.
(c ) For which frequencies of the source is the power transferred to the circuit half the power at resonant frequency?
(d) What is the Q-factor of the circuit?View Solution
Knowledge Check
- Question 1 - Select One
A series LCR circuit with R=20Ω,L=1.5H and C=35μF is connected to a variable frequency 200V ac supply. When the frequency of the supply equals the natural frequency of the circuit, what is the average power in kW transferred to the circuit in one complete cycle?
A200 WB2000 WC100 WD4000 W - Question 2 - Select One
A series LCR circuit with R=22Ω,L=1.5H and C=40μF is connected to a variable frequency 220 V ac supply. When the frequency of the supply equals the natural frequency of the circuit, what is the average power transferred to the circuit in one complete cycle?
A2000 WB2200 WC2400 WD2500 W - Question 3 - Select One
A series LCR circuit has R=5Ω,L=40mH and C=1μF, the bandwidth of the circuit is
A10 HzB20 HzC30 HzD40 Hz
An inductor L and a capacitor C are connected in the circuit as shown in the figure. The frequency of the power supply is equal to the resonant frequency of the circuit. Which ammeter will read zero ampere
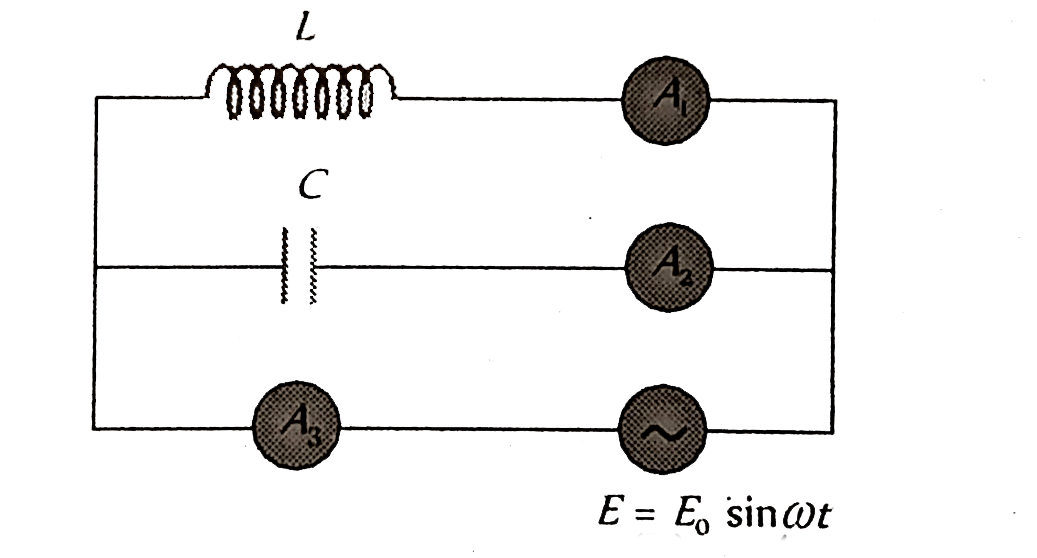 View Solution
View SolutionA series LCR circuit with L=4.0H,C=100μF and R=60Ω is connected to a variable frequency 240 V source. Calculate
(i) angular frequency of the source which drives the circuit in resonance,
(ii) current at the resonating frequency,
(iii) rms potential drop across the inductance at resonance.View SolutionAn LCR series circuit with L=100mH,C=100μF,R=120Ω is connected to an AC source of emfε=(30V)sin(100s−1)t. Find the impedane, the peak current and the resonant frequency of the circuit.
View SolutionIn an L−C−R ereis circuit R=150Ω,L=0.0750H and C=0.0180μF . The source has voltage amplitude V=150V and a frequencey equal to the resonacne frequency of the circuit.
(a) What is the power factor ?
(b) What is the average power delivered by the source?
(c) The capacitor is replaced by one with C=0.0360μF and the source frequency is adjusted to the new resonance value. Then, what is the average power delivered by the source?View SolutionSuppose the circuit in Exercise 7.18 has a resistance of 15Ω Obtain the average power transferred to each element of the circuit, and the total power absorbed.
View Solution

