At what angle should a ray of light be incident on the face of a prism of refracting angle 60∘, so that it just suffers total internal reflection at the other face ? The refractive index of the prism is 1.524.
The incident, refracted, and emerged rays associated with a glass prism ABC are shown in the figure.
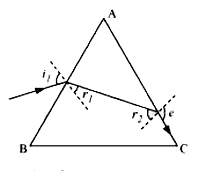
Angle of prim, A=60∘. Refractive index of the prism, μ=1.524
i1 = Incident angle
r1 = Refracted angle
r2 = Angle of incidence at the face AC
e=Emergent anlge = 90∘ According to Snell's law ,f for face AC, we can have:
sinesinr2=μ
sinr2=1μ×sin90∘
=11.524=0,6562
∴r1=A−r2=60−41=19∘
Accoridng to the Snell's law, we have the relation:
μ=sini1sinr1
sini1=μsinr1
=1.524×sin19∘=0.496
∴i1=29.75∘
Hence, the angle of incidence is 29.75∘.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Exercise
32 Videos
- NUCLEIBOOK - NCERT ENGLISHCHAPTER - NUCLEIEXERCISE - Exercise
31 Videos
- SEMICONDUCTOR ELECTRONICS MATERIALS DEVICES AND SIMPLE CIRCUITSBOOK - NCERT ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS MATERIALS DEVICES AND SIMPLE CIRCUITSEXERCISE - Exercise
15 Videos
Similar Questions
At what angle should a ray of light be incident on the face of a prism of refracting angle 60° so that it just suffers total internal reflection at the other face ? The refractive index of the material of the prism is 1.524.
View SolutionA ray of light is incident on a glass prism of refractive index μ and refractive angle A. If it just suffers total internal reflection at the other face, obtain an expression relating the angle of incidence , angle of prism and critical angle.
View Solution
Knowledge Check
A ray of light is incident at an angle of 60∘ on one face of a prism of angle 30∘. They ray emerges normally from the other face of the prism. The refractive index of the prism material is
A√2B√3C2D3A ray of light is incident at 60∘ on one face of a prism of angle 30∘ and the emergent ray makes 30∘ with the incident ray. The refractive index of the prism is
A1.732B1.414C1.5D1.33A ray of light is incident at 60∘ on one face of a prism of angle 30∘ and the emergent ray makes 30∘ with the incident ray. The refractive index of the prism is
A1.732B1.414C1.5D1.33
A ray of light is incident on a glass prism of refractive index μ and refractive angle A. If it just suffers total internal reflection at the other face, obtain an expression relating the angle of incidence , angle of prism and critical angle.
View SolutionCalculate the angle of incidence on the face of a prism of refracting angle 60∘ and of refractive index 1.5, for which the emergent ray just grazes the other face.
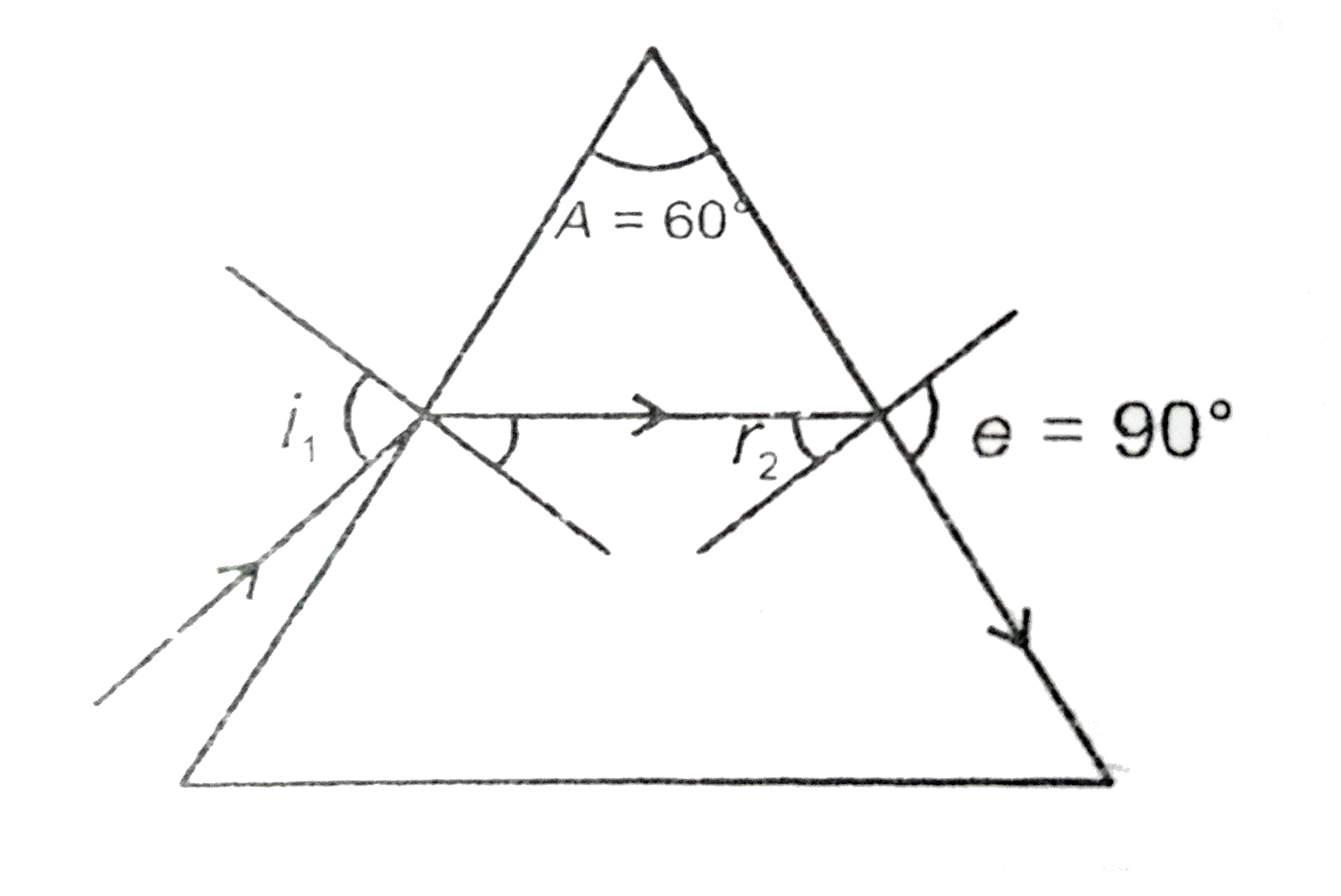
View SolutionCalculate the angle of incidence on the face of a prism of refracting angle 60∘ and of refractive index 1.5, for which the emergent ray just grazes the other face.

View SolutionA ray of light is incident at 60∘ on one face of a prism of angle 30∘ and the emergent ray makes 30∘ with the incident ray. The refractive index of the prism is
View SolutionA ray of light incident normally on the first face of a glass prism of refractive index 1.6 just emerges from the other face. Find the angle of the prism.
View Solution
