You are riding an automobile of mass 3000kg. Assuming that you are examining the oscillation characteristics of its suspension system. The suspension sags 15cm when the entire automobile is placed on it. Also, the amplitude of oscillation decreases by50% during one complete oscillation. Estimate the values of (a) the spring constant k and (b) damping constant b for the spring and shock absorber system of one wheel, assuming that each wheel supports 750kg.g=10m/s2.
To solve the problem step by step, we will first determine the spring constant k and then the damping constant b.
Step 1: Calculate the Spring Constant k
1. Identify the given values:
- Mass of the automobile M=3000kg
- Each wheel supports m=M4=30004=750kg
- The sag of the suspension x=15cm=0.15m
- Acceleration due to gravity g=10m/s2
2. Use Hooke's Law:
The force exerted by the spring is given by Hooke's Law:
F=kx
The weight of the automobile acting on the spring is:
F=mg=750×10=7500N
3. Set the forces equal:
mg=kx⟹k=mgx
4. Substitute the values:
k=75000.15=50000N/m=5×104N/m
Step 2: Calculate the Damping Constant b
1. Identify the amplitude decrease:
The amplitude decreases by 50% during one complete oscillation, meaning:
x=x02
2. Use the damping formula:
The displacement of a damped oscillator is given by:
x=x0e−bt2m
Setting x=x02:
x02=x0e−bt2m
Dividing both sides by x0 (assuming x0≠0):
12=e−bt2m
3. Take the natural logarithm:
ln(12)=−bt2m⟹−ln(2)=−bt2m
Rearranging gives:
b=2mln(2)t
4. Calculate the time period t:
The time period T of a mass-spring system is given by:
T=2π√mk
Substituting m=750kg and k=50000N/m:
T=2π√75050000=2π√0.015≈0.77s
5. Substitute T into the damping equation:
b=2×750×ln(2)0.77
Calculating ln(2)≈0.693:
b≈1500×0.6930.77≈1351.58kg/s
Final Answers:
- (a) The spring constant k=5×104N/m
- (b) The damping constant b≈1351.58kg/s
- Mass of the automobile M=3000kg
- Each wheel supports m=M4=30004=750kg
- The sag of the suspension x=15cm=0.15m
- Acceleration due to gravity g=10m/s2
The force exerted by the spring is given by Hooke's Law:
F=kx
The weight of the automobile acting on the spring is:
F=mg=750×10=7500N
mg=kx⟹k=mgx
k=75000.15=50000N/m=5×104N/m
The amplitude decreases by 50% during one complete oscillation, meaning:
x=x02
The displacement of a damped oscillator is given by:
x=x0e−bt2m
Setting x=x02:
x02=x0e−bt2m
Dividing both sides by x0 (assuming x0≠0):
12=e−bt2m
ln(12)=−bt2m⟹−ln(2)=−bt2m
Rearranging gives:
b=2mln(2)t
The time period T of a mass-spring system is given by:
T=2π√mk
Substituting m=750kg and k=50000N/m:
T=2π√75050000=2π√0.015≈0.77s
b=2×750×ln(2)0.77
Calculating ln(2)≈0.693:
b≈1500×0.6930.77≈1351.58kg/s
- (a) The spring constant k=5×104N/m
- (b) The damping constant b≈1351.58kg/s
Topper's Solved these Questions
Similar Questions
Knowledge Check
What is the mechanical equivalent of spring constant k in LC oscillating circuit?
A1LB1CCLCD1LCA system of springs with their spring constants are as shown in figure. What is the frequency of oscillations of the mass m ?
 A12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k4]mB12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mC12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mD12π√(k1+k2)(k3+k4)+k1k2k1k2(k3+k4)m
A12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k4]mB12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mC12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mD12π√(k1+k2)(k3+k4)+k1k2k1k2(k3+k4)m
Find the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.

View SolutionA spring mass system oscillates in a car. If the car accelerates on a horizontal road, the frequency of oscillation will
View SolutionFind the time period of the oscillation of mass m in figure a,b,c what is the equivalent spring constant of the pair oif springs in each case?
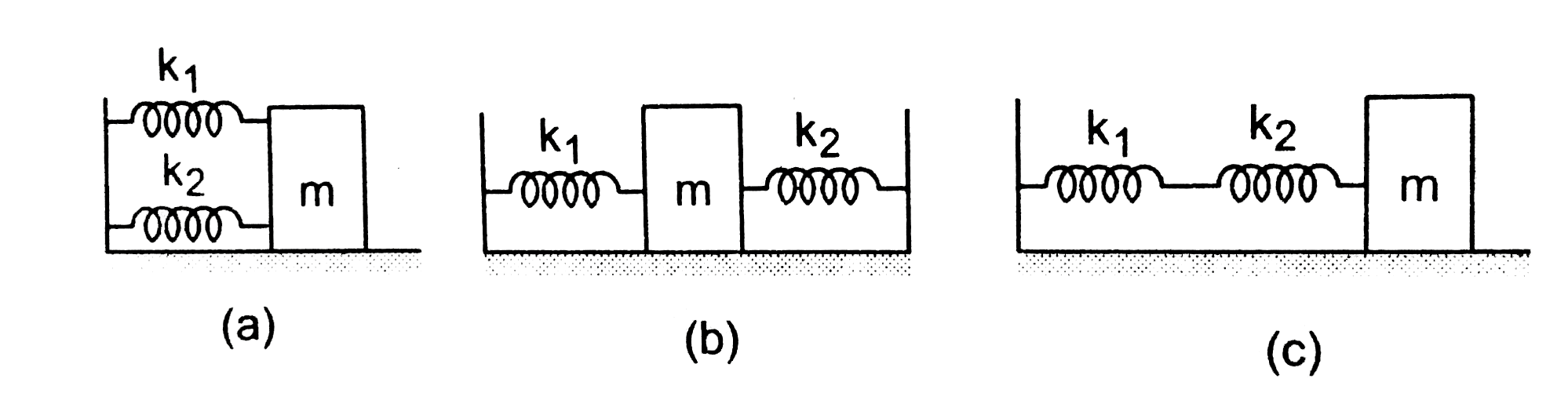
View SolutionFor the small damping oscillator, the mass of the block is 500 g and value of spring constant is k = 50 N/m and damping constant is 10gs^(-1) The time period of oscillation is (approx.)
View SolutionWhen an oscillator completes 50 oscillations its amplitude reduced to half of initial value (A0). The amplitude of oscillation, when it completes 150 oscillations is
View SolutionComparing the L-C oscillations with the oscillations of a spring-block system (force constant of spring=k and mass of block=m), the physical quantity mk is similar to
View Solution
