Comparing the L-C oscillations with the oscillations of a spring-block system
L is equivalent to m
C is equivalent to K
current is equivalent to speed
rate of change of current is equivalent to accelerate
The correct Answer is:A, C, D
To compare L-C oscillations with the oscillations of a spring-block system, we can analyze the equations governing both systems and identify their similarities and differences.
1. Understanding L-C Oscillation:
- An L-C circuit consists of an inductor (L) and a capacitor (C) connected together. When the circuit is closed, the capacitor discharges through the inductor, creating oscillations.
- The charge (Q) on the capacitor and the current (I) in the circuit are related. The governing equation for the L-C circuit can be derived using Kirchhoff's voltage law (KVL):
Ldidt+QC=0
- The current (I) can be expressed as the rate of change of charge (Q), so we can rewrite the equation as:
Ld2Qdt2+QC=0
- This is a second-order differential equation representing L-C oscillations.
2. Understanding Spring-Block Oscillation:
- A spring-block system consists of a mass (m) attached to a spring with spring constant (k). When the mass is displaced from its equilibrium position, it experiences a restoring force.
- The governing equation for the spring-block system is given by:
md2xdt2+kx=0
- Here, x is the displacement from the equilibrium position, and this is also a second-order differential equation representing simple harmonic motion (SHM).
3. Comparing the Two Systems:
- Both equations are second-order differential equations that describe oscillatory motion.
- By comparing the equations:
- For the L-C circuit: Ld2Qdt2+QC=0
- For the spring-block system: md2xdt2+kx=0
4. Identifying Analogies:
- From the comparison, we can establish the following analogies:
- Inductance (L) is analogous to mass (m).
- The spring constant (k) is analogous to 1C (inverse of capacitance).
- Charge (Q) is analogous to displacement (x).
- Current (I) is analogous to velocity (v=dxdt).
- The rate of change of current (didt) is analogous to acceleration (d2xdt2).
5. Conclusion:
- The L-C oscillation and the spring-block oscillation exhibit similar mathematical forms, indicating that they are analogous systems. The relationships established allow us to draw parallels between electrical and mechanical oscillations.
- An L-C circuit consists of an inductor (L) and a capacitor (C) connected together. When the circuit is closed, the capacitor discharges through the inductor, creating oscillations.
- The charge (Q) on the capacitor and the current (I) in the circuit are related. The governing equation for the L-C circuit can be derived using Kirchhoff's voltage law (KVL):
Ldidt+QC=0
- The current (I) can be expressed as the rate of change of charge (Q), so we can rewrite the equation as:
Ld2Qdt2+QC=0
- This is a second-order differential equation representing L-C oscillations.
- A spring-block system consists of a mass (m) attached to a spring with spring constant (k). When the mass is displaced from its equilibrium position, it experiences a restoring force.
- The governing equation for the spring-block system is given by:
md2xdt2+kx=0
- Here, x is the displacement from the equilibrium position, and this is also a second-order differential equation representing simple harmonic motion (SHM).
- Both equations are second-order differential equations that describe oscillatory motion.
- By comparing the equations:
- For the L-C circuit: Ld2Qdt2+QC=0
- For the spring-block system: md2xdt2+kx=0
- From the comparison, we can establish the following analogies:
- Inductance (L) is analogous to mass (m).
- The spring constant (k) is analogous to 1C (inverse of capacitance).
- Charge (Q) is analogous to displacement (x).
- Current (I) is analogous to velocity (v=dxdt).
- The rate of change of current (didt) is analogous to acceleration (d2xdt2).
- The L-C oscillation and the spring-block oscillation exhibit similar mathematical forms, indicating that they are analogous systems. The relationships established allow us to draw parallels between electrical and mechanical oscillations.
Similar Questions
While comparing the L−C oscillations with the oscillations of spring-block system, with whom the magnetic energy can be compared and why?
View SolutionComparing L-C oscillation with the oscillation if spring-block-system, match the following table.
Comparing L-C oscillations with the oscillations of spring-block sytem, match the following table Table-1(LC oscillations)Table-2(Spring-block oscillations)(A)L(P)k(B)C(Q)m(C)i(R)v(D)didt(S)x(T)None
View SolutionIn L − C oscillations
View SolutionAssertion : All small oscillation are simple harmonic in nature.
Reason : Oscillation of spring block system are always simple harmonic whether amplitude is small or large.
View SolutionA: If a spring block system, oscillating in a vertical plane is made to oscillate on a horizontal surface, the time period will remain same.
R: The time period of spring block system does not depend on g.
View Solution
A block of mass m is suspended from a spring and executes vertical SHM of time period T as shown in Fig. The amplitude of the SHM is A and spring is never in compressed state during the oscillation. The magnitude of minimum force exerted by spring on the block is
View Solution
A block A of mass m is placed on a smooth horizontal platform P and between two elastic massless springs S1 and S2 fixed horizontally to two fixed vertical walls. The elastic constants of the two springs are equal to k and the equilibrium distance between the two springs both in relaxed states is d. The block is given a velocity v0 initially towards one of the springs and it then oscillated between the springs. The time period T of oscillations and the minimum separation dm of the spring will be
View SolutionThe ratio of the time periods of small oscillation of the insulated spring and mass system before and after charging the masses is
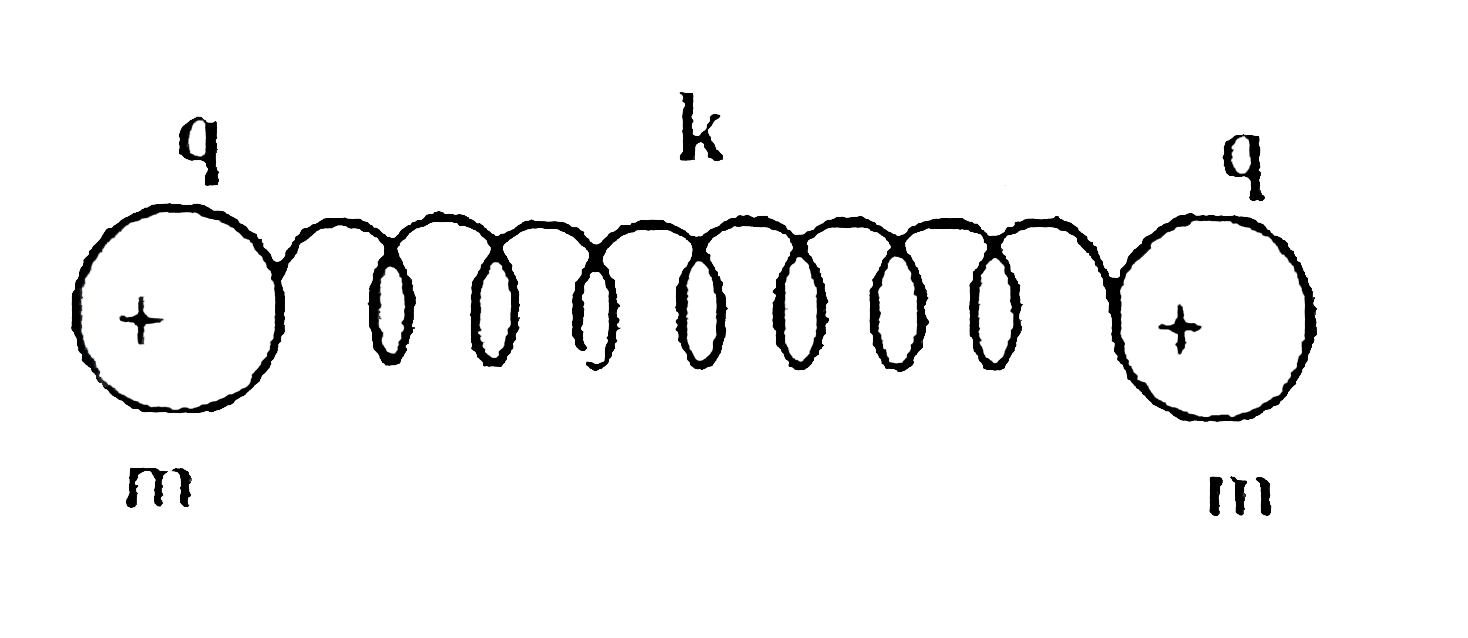
View Solution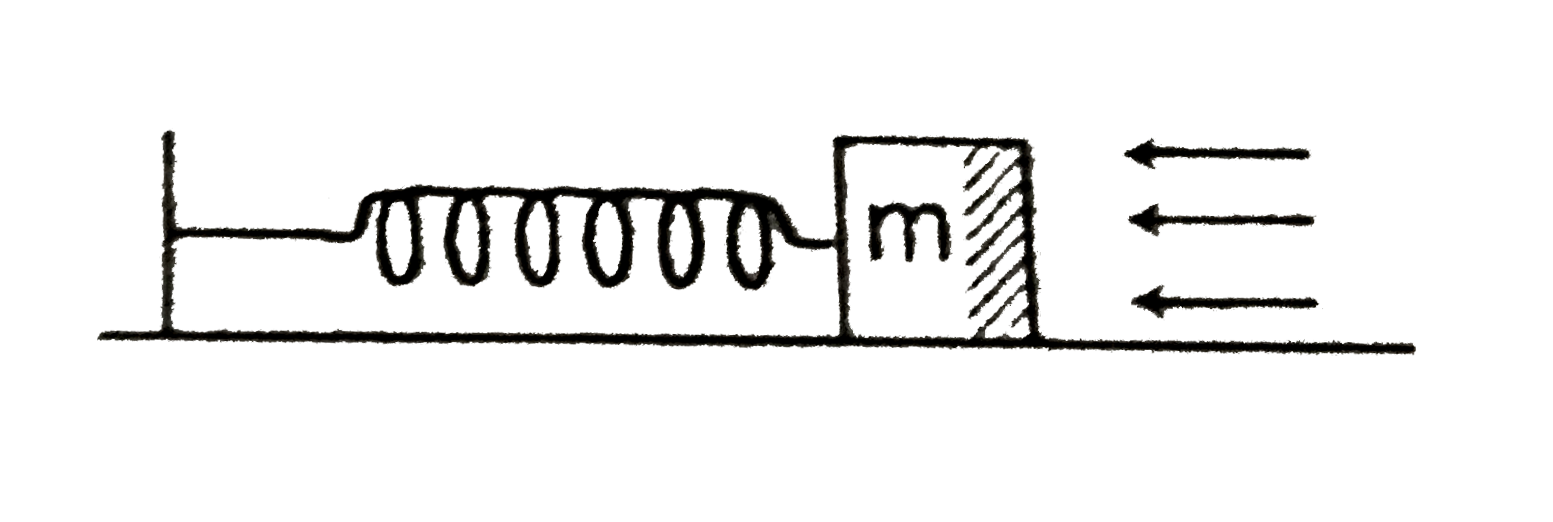
A spring block system with mass of block m and spring constant K (all the surfaces of blocks are perfectly abosrbing and smooth) is placed on a smooth horizontal plane as shown in the diagram at rest. A light beam of intensity l is switched on its right side. find the amplitude of oscillations of the block. (face area of block is A and c is the speed of light in vacuum)
View SolutionA spring-block system undergoes vertical oscillations above a large horizontal metal sheet with uniform positive charge. The time period of the oscillations is T. If the block is given a charge Q, its time period of oscillation will be
View Solution
