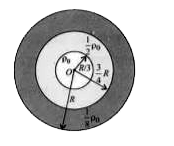
त्रिज्या R के एक विषमांगी गोले में निम्न घनत्व भिन्नताएँ हैं-
ρ=ρ0,r≤R3
=12ρ0,R3<r≤3R4
=18ρ0,3R4<r≤R
गोले के केन्द्र से 2R दूरी पर गुरुत्वीय क्षेत्र क्या होगा?
0.1πGRρ0
0.2πGRρ0
0.3πGRρ0
0.4πGRρ0
The correct Answer is:A
गोले के केन्द्र से 2R दूरी पर गुरुत्वीय क्षेत्र,
E=GM(2R)2
जहाँ M सम्पूर्ण गोले का द्रव्यमान है।
यहाँ , M=43π(R3)3ρ0+{43π(34R)3−43π(R3)3}ρ02+{43πR3−43π(34R)3}ρ08
=43πR3ρ0{127+27128−154+18−27512}
=43πR3ρ0{512+2916−256+1728−72913824}
=43πR3ρ0{5156−98513824}=43πR3ρ0{417113824}
=0.402πR3ρ0
∴E=G(0.402πR3ρ0)(2R)2=0.1πGRρ0
Topper's Solved these Questions
- गुरुत्वाकर्षण BOOK - NCERT FINGERTIPS HINDICHAPTER - गुरुत्वाकर्षण EXERCISE - एन. सी. ई. आर. टी. प्रश्न प्रदर्शिका
8 Videos
- गुरुत्वाकर्षण BOOK - NCERT FINGERTIPS HINDICHAPTER - गुरुत्वाकर्षण EXERCISE - अभिकथन एवं तर्क प्रारूप प्रश्न
15 Videos
- गति के नियम BOOK - NCERT FINGERTIPS HINDICHAPTER - गति के नियम EXERCISE - अभिकथन एवं तर्क प्रारूप प्रश्न
15 Videos
- ठोसों के यांत्रिक गुणBOOK - NCERT FINGERTIPS HINDICHAPTER - ठोसों के यांत्रिक गुणEXERCISE - अभिकथन एवं तर्क प्रारूप प्रश्न
15 Videos
Similar Questions
पृथ्वी लगभग गोल है। यदि अंदर का पदार्थ जिसका समस्त स्थानों पर घनत्व समान नहीं होता है, तब पृथ्वी की सतह पर गुरुत्वीय त्वरण
View Solutionअभिकथनः गोलीय कवच के अन्दर किसी कण का गुरुत्वाकर्षण बेल शून्य होता है।
तर्क: कवच अन्य पिण्डों को बाहर से अंदर कण पर गुरुत्वीय बल डालने से रक्षा करता है।
View Solutionअभिकथन: किसी वस्तु की गति को बनाए रखने के लिए एक बाहरी बल की आवश्यकता होती है।
तर्क: कुल बाह्य बल शून्य है तो विरामावस्था वाली वस्तु विरामावस्था में ही रहेगी तथा गतिमान वस्तु एकसमान वेग से गतिमान रहती है।
View Solutionअभिकथनः यदि हम किसी पुट्टी (Putty) या मिट्टी के लोंदे पर बल को आरोपित करते हैं तो उनमें पूर्व की आकृति को फिर से प्राप्त करने की कुल प्रवृत्ति नहीं होती है।
तर्कः इस प्रकार के पदार्थ अभिघट्य पदार्थ कहलाते हैं।
View SolutionA non-homogenous sphere of radius R has the following density variation.
ρ=ρ0,r≤r/3,
ρ=ρ0/2,R3<r≤3R4,
ρ=ρ08,(3R)/(4)<r≤R,
What is the gravitational field due to sphere at distance 2R from center?
View SolutionA non-homogeneous sphere of radius R has the following density variation : rho{{:(rho_(0),rleR//3),(rho_(0)//2,(R//3) lt r le (3R//4)),(rho_(0)//8,(3R//4) lt r le R):} The gravitational field at a distance 2R from the centre of the sphere is
View SolutionWrite the following as intervals :
(i) {x:x∈R,−4<x≤6}
(ii) {x:x∈R,−12<x<−10}
(iii) {x:x∈R,0≤x<7}
(iv) {x:x∈R,3≤x≤4}.
View SolutionExpress each of the following sts as an interval :
(i)A={x:x∈R,−4,<x<0}
(ii)B={x:x∈R,0≤x<3}
(iii)C={x:x∈R,2<x≤6}
(iv)D={x:x∈R,−5≤x≤2}
(v)E={x:x∈R,−3≤x<2)
(vi)F={x:x∈R,−2,≤x<0}
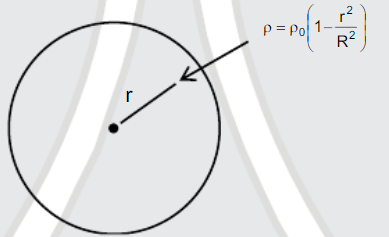
View SolutionThe volume charge density in a spherical ball of radius R varies with distance r from the centre s ρ(r)=ρ0[1−(rR)3] where ρ0 is a constant. The radius at which the field be maximum is
View SolutionMass density of sphere having radius R varies as ρ=ρ0(1−r2R2) . Find maxium magnitude of gravitational field
View Solution2≤r≤n के लिए (nr)+2(nr−1)+(nr−2) =
View SolutionCharge density of a sphere of radius R is rho = rho_0/r where r is distance from centre of sphere.Total charge of sphere will be
View Solutionनिम्न सम्मुच्यों को अंतराल के रूप में लिखो?
(i) {x:x∈R,−2≤x<1}
(ii) {x:x∈R,−3<x≤2}
(iii) {x:x∈R,−3≤x≤−1}
(iv) {x:x∈R,−2<x<3}
View Solutionनिम्नलिखित को अंतराल में लिखिए:
(i) {x:x∈R,−4<x≤6}
(ii) {x:x∈R,−12<x<−10}
(iii) {x:x∈R,0≤x<7}
(iv) {x:x∈R,3≤x≤4}
View SolutionMass density of sphere having radius R varies as ρ=ρ0(1−r2R2) . Find maxium magnitude of gravitational field

View Solution
