Mass density of sphere having radius R varies as . Find maxium magnitude of gravitational field 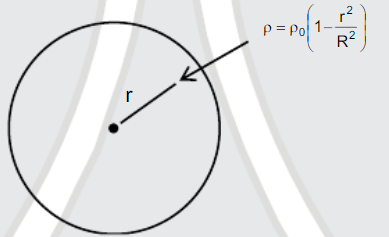
The correct Answer is:C
Step by step video & image solution for Mass density of sphere having radius R varies as rho = rho_0(1-r^2/R^2) . Find maxium magnitude of gravitational field by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.

View SolutionThe mass density of a planet of radius R varie with the distance r form its centre as ρ(r)=p0(1−r2R2). Then the graviational field is maximum at :
View SolutionCharge density of a sphere of radius R is ρ=ρ0r where r is distance from centre of sphere.Total charge of sphere will be

View SolutionThe density of a thin rod of length l varies with the distance x from one end as ρ=ρ0x2l2. Find the position of centre of mass of rod.
View SolutionThe distance between the centres of the Moon and the earth is D. The mass of the earth is 81 times the mass of the Moon. At what distance from the centre of the earth, the gravitational force will be zero?
View SolutionConsider a solid sphere oF radius R and mass density ρ(r)=ρ0(1−r2R2) 0<r≤R. The minimum density oF a liquid in which it will Float is:
View SolutionA non-conducting sphere of radius R has a spherical cavity of radius R/2 as shown. The solid part of the sphere has a uniform volume charge density ρ. Find the magnitude and direction of electric field at point (a) O and (b) A.

View SolutionThe density inside a solid sphere of radius a is given by ρ=ρ0r, where ρ0 is the density at the surface and r denotes the distance from the centre. Find the gravitational field due to this sphere at a distance 2a from its centre.
View SolutionConsider a sphere of radius R which carries a uniform charge density ρ. If a sphere of radius R2 is carved out of it,as shown, the ratio →EA→EB of magnitude of electric field →Ea and →EB, respectively, at points A and B due to the remaining portion is:
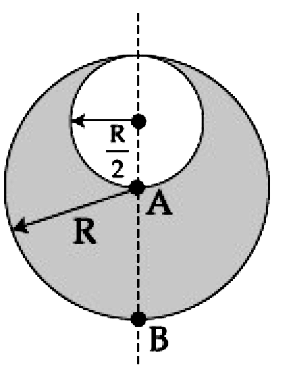
View SolutionThe density inside a solid sphere of radius a is given by ρ=ρ0r, where ρ0 is the density ast the surface and r denotes the distance from the centre. Find the graittional field due to this sphere at a distance 2a from its centre.
View Solution
