The circum-centre of a triangle ABC is O. If ∠BAC=85∘, ∠BCA=75∘, then ∠OAC is of
70∘
72∘
75∘
74∘
The correct Answer is:A
To find the angle OAC in triangle ABC with given angles ∠BAC=85∘ and ∠BCA=75∘, we can follow these steps:
Step 1: Calculate ∠ABC
We know that the sum of angles in a triangle is 180∘. Therefore, we can find ∠ABC as follows:
∠ABC=180∘−∠BAC−∠BCA
Substituting the given values:
∠ABC=180∘−85∘−75∘=20∘
Step 2: Understanding the Angles at the Circumcenter
The circumcenter O of triangle ABC is the point where the perpendicular bisectors of the sides intersect. The angle OAC is related to the angles at the vertices of the triangle.
Step 3: Relate ∠OAC to ∠ABC
The angle OAC is half of the angle ABC because the angle subtended at the center (which is O) is twice that at the circumference (which is A). Therefore, we can express this relationship as:
∠OAC=12×∠ABC
Step 4: Substitute the Value of ∠ABC
Now, substituting the value we found for ∠ABC:
∠OAC=12×20∘=10∘
Step 5: Conclusion
Thus, the angle OAC is 10∘.
Final Answer
∠OAC=10∘
---
We know that the sum of angles in a triangle is 180∘. Therefore, we can find ∠ABC as follows:
Substituting the given values:
The circumcenter O of triangle ABC is the point where the perpendicular bisectors of the sides intersect. The angle OAC is related to the angles at the vertices of the triangle.
The angle OAC is half of the angle ABC because the angle subtended at the center (which is O) is twice that at the circumference (which is A). Therefore, we can express this relationship as:
Now, substituting the value we found for ∠ABC:
Thus, the angle OAC is 10∘.
∠OAC=10∘
Similar Questions
Knowledge Check
O is the circumcentre of the triangle ABC and ∠BAC=85∘, ∠BCA=75∘ , then the value of ∠OAC is
A55∘B150∘C20∘D70∘If in a ΔABC,∠A=45∘,∠B=75∘, then
Aa+c√3=2bBa+c=2bCa+c√2=2bDa−c=2bO is the circumcentre of the △ABC. If ∠BAC=50∘, then ∠OBC is equal to
A30∘B60∘C40∘D50∘
In a ΔABC,∠A=65∘,∠C=75∘, where O is circumcentre , find ∠OAC.
View SolutionIf O is the circumcenter of △ABC and ∠OBC=35∘, then the ∠BAC is equal to
यदि O, △ABC का परिकेन्द्र है और ∠OBC=35∘ तो ∠BAC बराबर है-
View SolutionIn the figure, O is centre of a circle. If ∠BAC=20∘and∠ACB=30∘. Find ∠AOC
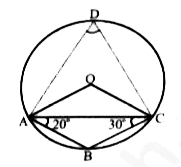
View SolutionO is the circumcentre of ΔABC, given ∠BAC=85∘and∠BCA=55∘, find ∠OAC.
View SolutionIf O is the incentre of a triangle ABC and ∠AOC=124∘, find the ∠ABC.
View Solution
