If x=am.bncp.dq then the percentages error in the measurement of x,
Δxx=m(ΔaA)+n(Δbb)+p(Δcc)+q(Δdc)
(R) : The above is true for all values or Δa,Δb,Δc and Δd.
Both (A) and (R) are true and (R) is the correct explanation of (A)
Both (A) and (R) are true and (R) is not the correct explanation of (A)
(A) is true but (R) is false
Both (A) and (R) are false
The correct Answer is:C
Topper's Solved these Questions
- UNITS AND MEASUREMENTSBOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTSEXERCISE - EXERCISE -2
56 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTSEXERCISE - EXERCISE -3
66 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTSEXERCISE - EXERCISE -1 A
187 Videos
- UNITS AND MEASUREMENTBOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTEXERCISE - PRACTICE EXERCISE
45 Videos
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - PRACTICE SHEET ADVANCED (INTEGER TYPE QUESTIONS)
10 Videos
Similar Questions
Knowledge Check
If Q=xnymandΔx,Δy are absolute errors in the measurement of x and y then absolute error ΔQ in Q is
AΔQ=±(nΔxx+mΔyy)BΔQ=±(nΔxx+mΔyy)QCΔQ=±(nΔxx−mΔyy)QDΔQ=±(nΔxy−mΔyx)QIf ∣∣ ∣ ∣∣abclmnpqr∣∣ ∣ ∣∣=2, then what is the value of the determinant ∣∣ ∣ ∣∣6a3b15c2lm5n2pq5r∣∣ ∣ ∣∣ = ?
A10B20C40D60If ∣∣ ∣ ∣∣abclmnpqr∣∣ ∣ ∣∣=2, then what is the value of the determinant ∣∣ ∣ ∣∣6a3b15c2lm5n2pq5r∣∣ ∣ ∣∣?
A10B20C40D60
As is known, the result of an experiment is calculated by performing mathematical operation (like addition, subtraction, multiplication, division, etc.) on several measurements, which have different degrees of accuracy. It has been established that (a) When x=a+b,Δx=±(Δa+Δb)
(b) When x=a−b,Δx=±(Δa+Δb)
(c ) When x=a×b,Δxx=±(Δaa+Δbb)
(d) When x=ab,Δxx=±(Δaa+Δbb)
Read the above paragraph and answer the following questions : (i) Why is absolute error in x=(a−b), sun of the absolute error in a and b ? (ii) Why is fractional error in x=ab , sun of fractional error in a and b ? (iii) What do you learn from this ?
View SolutionIn Figure altitudes AD and CE of A B C intersect each other at the point P. Show that:(i) ΔAEP~ΔCDP (ii) ΔABD~ΔCBE (iii) ΔAEP~ΔADB(iv) ΔPDC~ΔBEC
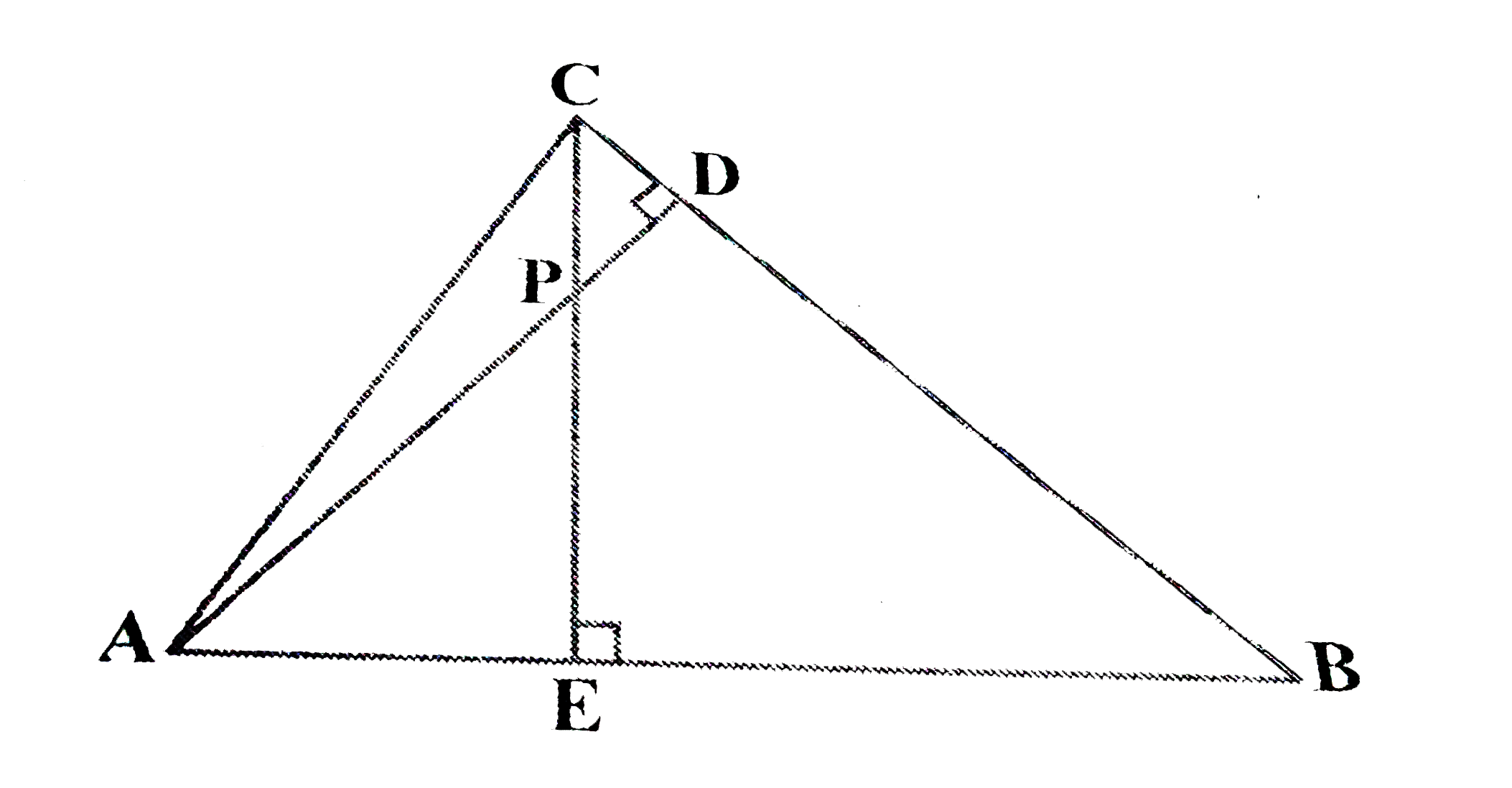
View SolutionIn Figure altitudes AD and CE of DABC intersect each other at the point P. Show that:
(i) ΔAEP~ΔCDP
(ii) ΔABD~ΔCBE
(iii) ΔAEP~ΔADB
(iv) ΔPDC~ΔBEC

View SolutionIn figure Cm and RN are respectively the medians of ΔABCand ΔPQR. If ΔABC~ΔPQR, prove that: (i) ΔAMC~ΔPNR (ii) CMRN=ABPQ (ii) ΔCMB~ΔRNQ
View SolutionIn figure Cm and RN are respectively the medians of ΔABCand ΔPQR. If ΔABC~ΔPQR, prove that:
(i) ΔAMC~ΔPNR
(ii) CMRN=ABPQ
(ii) ΔCMB~ΔRNQ

View Solution
