In figure Cm and RN are respectively the medians of ΔABCand ΔPQR. If ΔABC~ΔPQR, prove that: (i) ΔAMC~ΔPNR (ii) CMRN=ABPQ (ii) ΔCMB~ΔRNQ
To solve the given problem, we will follow the steps outlined in the video transcript and provide a detailed step-by-step solution.
Step 1: Prove ΔAMC∼ΔPNR
Since ΔABC∼ΔPQR, we have:
- ∠A=∠P
- ∠B=∠Q
- ∠C=∠R
Now, consider triangle AMC:
- ∠AMC=∠A (common angle)
- ∠ACB=∠PRN (since C corresponds to R)
Thus, by the Angle-Angle (AA) similarity criterion:
ΔAMC∼ΔPNR
Step 2: Prove CMRN=ABPQ
Since ΔABC∼ΔPQR, the ratio of the lengths of corresponding sides is equal:
ABPQ=ACPR=BCQR
Now, since CM and RN are medians, they divide the triangles into two smaller triangles. The lengths of the medians are proportional to the lengths of the sides of the triangles they belong to. Therefore:
CMRN=ABPQ
Step 3: Prove ΔCMB∼ΔRQN
Again, using the similarity of triangles ΔABC and ΔPQR:
- ∠C=∠R
- ∠B=∠Q
In triangle CMB:
- ∠CMB=∠C (common angle)
Thus, by the Angle-Angle (AA) similarity criterion:
ΔCMB∼ΔRQN
Conclusion
We have proved all three statements as required:
1. ΔAMC∼ΔPNR
2. CMRN=ABPQ
3. ΔCMB∼ΔRQN
---
- ∠A=∠P
- ∠B=∠Q
- ∠C=∠R
- ∠AMC=∠A (common angle)
- ∠ACB=∠PRN (since C corresponds to R)
ΔAMC∼ΔPNR
ABPQ=ACPR=BCQR
CMRN=ABPQ
- ∠C=∠R
- ∠B=∠Q
- ∠CMB=∠C (common angle)
ΔCMB∼ΔRQN
We have proved all three statements as required:
1. ΔAMC∼ΔPNR
2. CMRN=ABPQ
3. ΔCMB∼ΔRQN
Topper's Solved these Questions
- TRIANGLESBOOK - NCERT ENGLISHCHAPTER - TRIANGLESEXERCISE - Exercise 6.4
9 Videos
- TRIANGLESBOOK - NCERT ENGLISHCHAPTER - TRIANGLESEXERCISE - Exercise 6.1
3 Videos
- TRIANGLESBOOK - NCERT ENGLISHCHAPTER - TRIANGLESEXERCISE - Exercise 6.2
10 Videos
- SURFACE AREAS AND VOLUMESBOOK - NCERT ENGLISHCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - Exercise 13.3
9 Videos
Similar Questions
In figure, if ΔABE≅ΔACD, show that ΔADE~ΔABC.

View SolutionIf AD and PM are medians of triangles ABC and PQR, respectively whereΔABC~ΔPQR, prove that ABPQ=ADPM
View SolutionIn figure, if PQ||RS, prove that ΔPOQΔSOR.
View SolutionSides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ΔPQR. Show that ΔABC~ΔPQR.
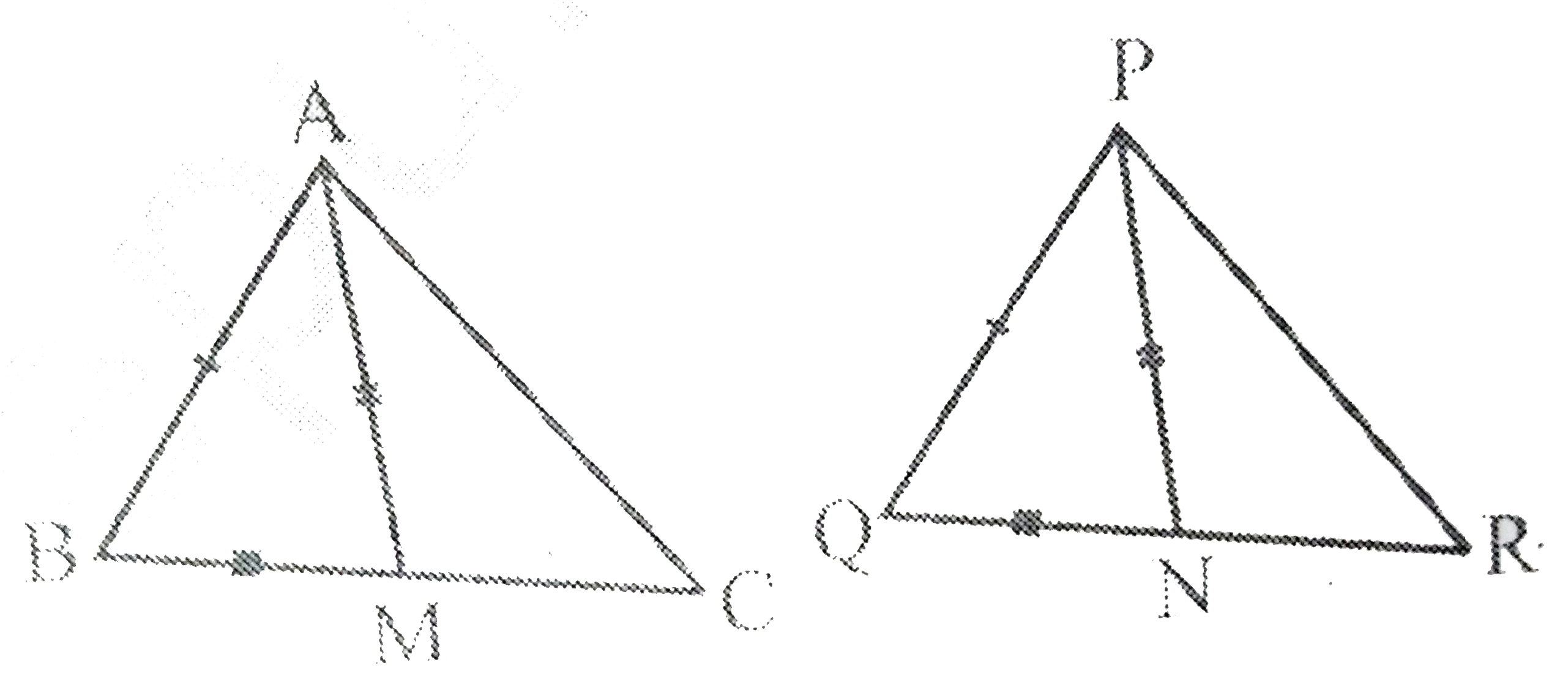
View SolutionTwo sides AB and BC and median AM of one triangle ABC are respectively equal to side PQ and QR and median PN of ΔPQR(see Fig. 7.40). Show that:
(i) ΔABM≅ΔPQN
(ii) ΔABC≅ΔPQR
View SolutionIn Fig. if PQ∣∣BC and PR∣∣CD . Prove that (i) ARAD=AQAB (ii) QBAQ=DRAR .
View SolutionIn figure ABC and AMP are two right triangles, right angles at B and M respectively. Prove that(i) ΔABC~ΔAMP (ii) CAPA=BCMP

View SolutionIf ΔABC~ΔPQR such that ar(ABC)=4ar(PQR). If BC=12cm , then QR=
View SolutionS and T are points on sides PR and QR of ΔPQR such that ∠P=∠RTS. Show that ΔRPQ~ΔRTS.
View SolutionIn △ABC, P and Q are respectively the mid-points of AB and BC and R is the mid-point of AP. Prove that: ar (△RQC)=38 ar (△ ABC).
View Solution
