A plane longitudinal wave having angular frequency ω = 500 rad /sec is travelling in positive x-direction in a medium of density ρ =1 kg/m and bulk modulus 4×104N/m2 . The loudness at a point in the medium is observed to be 20 dB. Assuming at x = 0 initial phase of the medium particles to be zero, find the equation of the wave
y=2×10−9sin(500t−5x2)
y=3×10−9sin(500t+5x2)
y=3×10−9sin(500t+5x2)
y=2×10−9sin(5000t−5x2)
The correct Answer is:A
Topper's Solved these Questions
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - LECTURE SHEET (EXERCISE-IV (LEVEL-II(ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS))
5 Videos
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - LECTURE SHEET (EXERCISE-IV (LEVEL-II(ADVANCED) MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS))
1 Videos
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - LECTURE SHEET (EXERCISE-III (LEVEL-II(ADVANCED) INTEGER TYPE QUESTIONS))
2 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTSEXERCISE - EXERCISE -3
66 Videos
- WAVE MOTION AND SOUNDBOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - II)
81 Videos
Similar Questions
A plane longitudinal wave of angular frequency ω=1000 rad Is is travelling along positive x direction in a homogeneous gaseous medium of density d=1kgm−3 . Intensity of wave is I=10−10W.m−2 and maximum pressure change is (ΔP)m=2×10−4Nm−2 . Assuming at x = 0, initial phase of medium particles to be zero
Velocity of the wave is
View SolutionA plane longitudinal wave of angular frequency ω=1000 rad/s is travelling along positive x direction in a homogeneous gaseous medium of density d=1kgm−3 . Intensity of wave is I=10−10W.m−2 and maximum pressure change is (ΔP)m=2×10−4Nm−2 . Assuming at x = 0, initial phase of medium particles to be zero
Amplitude of the travelling wave is
(a) 10−6m
(b) 10−7m
(c) 10−9m
(d) 2×10−8m
View Solution
Knowledge Check
A transverse wave, whose amplitude is 0.5 m wavelength is 1 m and frequency is 2Hz. is travelling along positive x direction. The equation of this wave will be-
Ay=0.5cos(2πx−4πt)By=0.5cos(2πx−4πt)Cy=0.5sin(πx−2πt)Dy=0.5cos(2πx−2πt)A plane wave is described by the equation y=3cos(x4−10t−π2). The maximum velocity of the particles of the medium due to this wave is
A30B3π2C3/4D40
Longitudinal waves of frequency 400Hz are produced in a rod of material of density 8000kg/m3 and Young modulus 7.2×1010N/m2. What is the wavelength of the wave?
View SolutionA sinusoidal wave travelling in the positive x direction has an amplitude of 15 cm, wavelength 40 cm and frequency 8 Hz. The vertical displacement of the medium at t =0 and x = 0 is also 15 cm, as shown
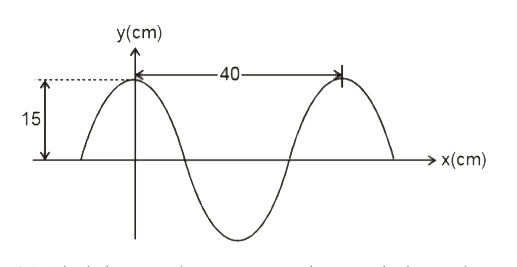
(a) Find the angular wave number, period angular frquency and speed of the wave.
View SolutionElectro magnetic waves travel in a medium with speed of 2×108m/sec. The relative permeability of the medium is 1 find relative permittivity.
View SolutionElectro magnetic waves travel in a medium with speed of 2×108m/sec. The relative permeability of the medium is 1 find relative permittivity.
View SolutionThe equation of a plane standing wave in a homogeneous elastic medium has the form ξ=acoskx.Cosωt. Plot :
(a) ξ and δξ/δx as functions of x at the moments t=0 and t=T/2, where T is the oscillation period,
(b) the distribution of density ρ(x) of the medium at the moments t=0 and t=T/2 in the case of longitudinal oscillation ,
(c) the velocity distribution of particles of the medium at the moment t=T/4 , indicate the directions of velocities at the antinodes, both for longitudinal and transverse oscillation.
View SolutionFind the intensity of sound wave whose frequency is 250 Hz. The displacement amplitude of particles of the medium at this position is 1×10−8 m. The density of the medium is 1kg/m3, bulk modulus of elasticity of the medium is 400N/m2.
View Solution
