The base AB of an equilateral Δ ABC of side 2p lies along the X-axis such that the midpoint of AB is at the origin and vertex C is above x-axis. Find coordinates of the vertices of Δ ABC. Solution in Kannada
The correct Answer is:A(-p, 0) , B (p,0).
Step by step video, text & image solution for The base AB of an equilateral Delta ABC of side 2p lies along the X-axis such that the midpoint of AB is at the origin and vertex C is above x-axis. Find coordinates of the vertices of Delta ABC. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CO-ORDINATE GEOMETRYBOOK - ZEN PUBLICATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - ZEN ADDITIONAL QUESTIONS - LONG ANSWER [LA] TYPE QUESTIONS
6 Videos
- CO-ORDINATE GEOMETRYBOOK - ZEN PUBLICATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - ZEN ADDITIONAL QUESTIONS - HIGHER ORDER THINKING SKILLS [HOTS] QUESTIONS
14 Videos
- CO-ORDINATE GEOMETRYBOOK - ZEN PUBLICATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - ZEN ADDITIONAL QUESTIONS - VERY SHORT ANSWER [VSA] TYPE QUESTIONS
14 Videos
- CIRCLESBOOK - ZEN PUBLICATIONCHAPTER - CIRCLESEXERCISE - ZEN ADDITIONAL QUESTIONS ( HOT [HIGHER ORDER THINKING SKILLS] - QUESTIONS) (IIT AND IMO)
9 Videos
- CONSTRUCTIONSBOOK - ZEN PUBLICATIONCHAPTER - CONSTRUCTIONSEXERCISE - ZEN ADDITIONAL QUESTIONS ( HOTS [HIGHER ORDER THINKING SKILLS] - QUESTIONS) IIT /OLYMPIAD/ IMO
5 Videos
Similar Questions
The vertices of AABC are A(4, 6), B(1, 5), and C7, 2). A line is drawn to intersect sides AB and AC at D and E respectively. Show that ADAB=AEAC=14. Find the area of Δ ADE and compare it with Δ ABC.
View SolutionIn what ratio does 4x +3y-13 0 divide the line segment joining (2, 1) and (1, 4)?
View SolutionFind the area of the triangle Δ ABC with A(a,b+c), B(b,c+a), and C(c, a+ b).
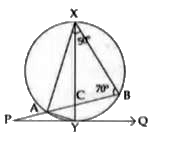
View SolutionIn the adjoining figure, XY is a diameter of the circle and PQ is a tangent to the circle at Y. Given that ⌊AXB=50∘ and ⌊ABX=70∘, calculate ⌊BAY and ⌊APY.
View SolutionGiven below are the steps of construction of a pair of tangents to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm. Find which of the following steps is wrong.
(P) Step 1: Take a point O on the plane paper and draw a circle of radius OA = 4 cm. Also draw a concentric circle of radius OB = 6 cm.
(Q) Step 2: Find the midpoint C of OB and draw a circle of radius BA= AO. Suppose this circle intersects the circle of radius 4 cm at P and Q.
(R) Step 3: Join BP and BQ to get the desired tangents.
View SolutionIf a is the length of one of the sides of an equilateral triangle ABC, base BC lies on x -axis and vertex B Is at the origin,find the co- ordinates of the vertices of the triangle.
View SolutionThe base of an equilateral triangle with side 20cm lies along x-axis such that the mid-point of the base is at the origin. Find the vertices of the triangle
View SolutionThe base BC of an equilateral triangle ABC, lies on y-axis. The coordinates of point C are (0, -3). The origin is the midpoint of the base.
Find the coordinates of the points A and B.
View Solutionएक समबाहु त्रिभुज की भुजा 5 है । शीर्षों के निर्देशांक ज्ञात कीजिए यदि आधार x - अक्ष पर हो और (i) एक शीर्ष मूलबिन्दु हो, (ii) आधार का मध्य बिन्दु मूलबिन्दु हो ।
View Solution2a भुजा के एक समबाहु त्रिभुज का आधार y− अक्ष के अनुदिश इस प्रकार है कि आधार का मध्य बिन्दु मूल बिन्दु पर है। त्रिभुज के शीर्ष ज्ञात कीजिए।
View Solutionदो समबाहु त्रिभुजों ABC और ABC' का आधार AB, x- अक्ष पर इस प्रकार स्थित है कि AB का मध्य बिन्दु मूल बिन्दु पर है जैसा कि चित्र 14.3 में दिखाया गया है । यदि AB=2a हो , तो त्रिभुजों के शीर्ष C और C' के निर्देशांक ज्ञात कीजिए ।
View SolutionThe side BC of an equilateral ΔABC is parallel to X - axis . Find the slopes of line along sides BC , CA and AB .
View SolutionThe base of an equilateral triangle with side 2a lies along the y-axis such that the mid-point of the base is at the origin. Find vertices of the triangle.
View SolutionFind the product of the following pairs?
9a2b,2a3b3
View SolutionThe base of an equilateral triangle with side 2a lies along the y-axis such that the mid-point of the base is at the origin. Find vertices of the triangle.
View Solution
