A pump holding water is designed as a horizontal cylinder with a piston having an area of A and an outlet orifice having an area of 'a' arranged near the cylinder axis.Determine the velocity of outflow of water in ms−1 from the pump is the piston moves with a constant velocity under the action of a force F ( A=2m2andF=4kN . Assume A>>a)
Step by step video & image solution for A pump holding water is designed as a horizontal cylinder with a piston having an area of A and an outlet orifice having an area of 'a' arranged near the cylinder axis.Determine the velocity of outflow of water in ms^(-1) from the pump is the piston moves with a constant velocity under the action of a force F ( A=2m^(2) and F=4kN . Assume A gt gt a) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Similar Questions
A pump is designed as a horizontal cylinder with a piston of areal A and and outlet orifice of areal a arranged mear the cylinder axis. Find the velocity of out flow of the liquid from the pump if the piston moves with a constant velocity under the action of a constant force F. The density of the liquid is ρ.
View SolutionA horizontal cylinder of length l contains water. On the left a constant force F is applied on the piston and on the right there is a small hole of area a. What is the velocity of the piston? Hence, calculate the work done in emptying the vessel in time t. brgt
given area of cylinder is A
View Solution
Knowledge Check
- Question 1 - Select One
Between a plate of area 100cm2 and another plate of area 100m2 there is a 1mm, thick layer of water, if the coefficient of viscosity of water is 0.01 poise, then the force required to move the smaller plate with a velocity 10cms−1 with reference to large plate is
A100dynB104dynC106dynD109dyn - Question 2 - Select One
A tank of height H and base area A is half filled with water and there is a small orifice at the bottom and there is a heavy solid cylinder having base area A3 and height of the cylinder is same as that of the tak. The water is flowing out of the orifice. Here cylinder is put into the tank to increase the speed of water flowing out.
After long time, when the height of water inside the tank again becomes equal to H2, the solid cylinder is taken out. then the velocity of liquid flowing out of the orifice (just after removing the cylinder) will beA√gH3B√3gH2C√2g(H3)D√2g(H2)
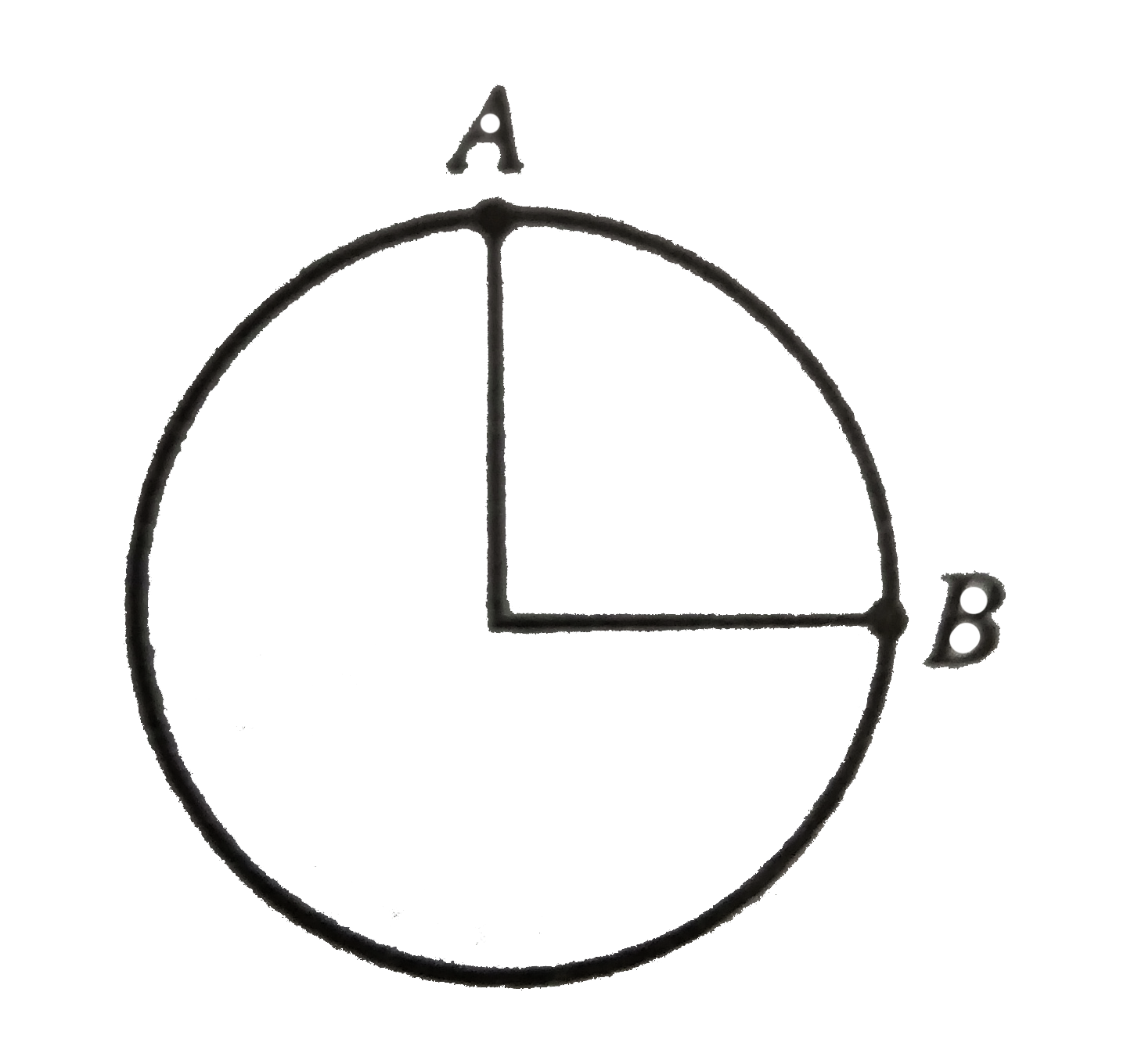
A particle is moving in a circular path of radius 1 m. under the action of a centripetal force, the speed √2πms−1 of the particle is constant. Find the average of the velocity (inms−1) between A and B.
View SolutionWhat work should be done in order to squeeze all water from a horizontally located cylinder (figure) during the time t by means of a constant force acting on the piston? The volume of water in the cylinder is equal to V, the cross-sectional area of the orifice to s, with s being considerably less than the piston area. The friction and viscosity are negligibly small.
View SolutionA hose directs a horizontal jet of water,moving with a velocity of 20m/s on to a vertical wall.The cross sectional area of the jet is 5×10−4m2 .If the force exerted by water jet on the wall is n×102N assuming the water is brought to rest there,find the value of n .
View SolutionA horizontal pipe of varying cross-sectional area carries water flowing at a constant rate. The pressure at sections (1) and (2) are 50cm and 20cm of Hg. If the velocity of section (1) is 5m/s, what is the velocity of section (2). Also determine the ratio of 4 areas at sections (1) and (2) (as shown in Fig.
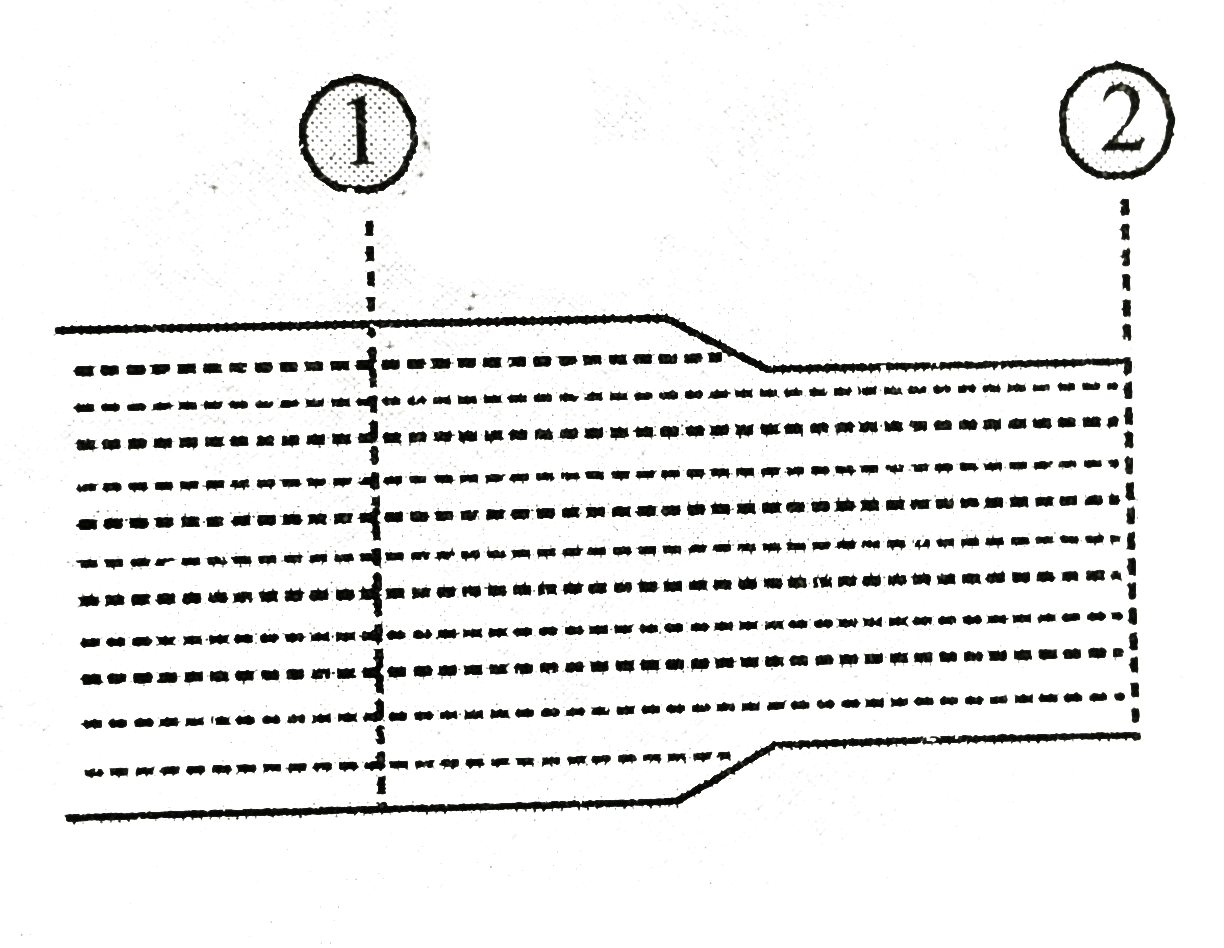View SolutionA area of cross section of a large tank is 0.5m2. It has an opening near the bottom having area of cross section 1cm2. A load of 20 kg is applied on the water at the top. Find the velocity of the water coming out of the opening at the time when the height of water level is 50 cm above the bottom. Take g=10ms−2
View SolutionA car of mass 1400 kg placed on the platform in a service station has to be lifted up. The area of the press piston to which the platform is 5m2. Determine the force that has to be applied on the piston of pump cylinder having an area of cross section 0⋅25m2.
(Take g = 10 m s−2)View Solution